Giải bài 31 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho lục giác đều ABCDEF cạnh bằng a. a) Chứng minh sáu điểm A, B, C, D, E, F cùng thuộc một đường tròn. Tính theo a bán kính của đường tròn đó. b) Chứng minh các tam giác ACE, BFD là các tam giác đều. Tính theo a bán kính đường tròn nội tiếp tương ứng của tam giác đó.
Đề bài
Cho lục giác đều ABCDEF cạnh bằng a.
a) Chứng minh sáu điểm A, B, C, D, E, F cùng thuộc một đường tròn. Tính theo a bán kính của đường tròn đó.
b) Chứng minh các tam giác ACE, BFD là các tam giác đều. Tính theo a bán kính đường tròn nội tiếp tương ứng của tam giác đó.
Phương pháp giải - Xem chi tiết
Dựa vào khoảng cách từ tâm đến các điểm trên đường tròn bằng nhau để chứng minh.
Dựa vào bán kính đường tròn ngoại tiếp tam giác đều \(r = \frac{a}{2}\) (a là cạnh tam giác đều).
Lời giải chi tiết
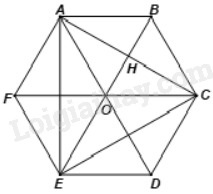
a) Vì ABCDEF là lục giác đều nên ba đường chéo chính AD, BE, CF bằng nhau và cắt nhau tại trung điểm O của mỗi đường, do đó OA = OB = OC = OD = OE = OF, nên sáu điểm A, B, C, D, E, F cùng thuộc đường tròn đường kính AD.
Vì ABCDEF là lục giác đều nên độ dài đường chéo chính AD gấp 2 lần độ dài cạnh, mà AD là đường kính của đường tròn đi qua sáu điểm A, B, C, D, E, F nên bán kính của đường tròn đi qua sáu điểm A, B, C, D, E, F bằng độ dài cạnh của lục giác đều và bằng a.
b) Vì ABCDEF là lục giác đều nên các góc ở các đỉnh của lục giác đều bằng nhau, suy ra \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EAF} = \widehat {AFB}\).
Vì ABCDEF là lục giác đều nên các cạnh bằng nhau, suy ra AB = BC = CD = DE = EF = FA.
Xét ∆ABC và ∆CDE có:
AB = CD
\(\widehat {ABC} = \widehat {CDE}\)
BC = DE
Do đó ∆ABC = ∆CDE (c.g.c)
Suy ra AC = CE (hai cạnh tương ứng).
Chứng minh tương tự, ta có kết quả AC = CE = AE = BD = DF = BF.
Do AC = CE = AE nên ∆ACE là tam giác đều.
Do BF = BD = DF nên ∆BFD là tam giác đều.
Gọi H là giao điểm của AC và OB.
Ta có OA = OB = AB = a nên ∆OAB là tam giác đều, do đó \(\widehat {ABO} = {60^o}\) hay \(\widehat {ABH} = {60^o}\).
Xét tứ giác OABC có OA = OC = AB = BC nên OABC là hình thoi, do đó hai đường chéo AC và OB vuông góc với nhau tại trung điểm H của mỗi đường.
Từ đó ta có AC = 2AH.
Xét ∆ABH vuông tại H, ta có:
AH = AB. sin \(\widehat {ABH}\) = a. sin 60 o = \(a\sqrt 3 \).
Vì ∆ACE là tam giác đều nên bán kính đường tròn nội tiếp của ∆ACE là \(\frac{{AC\sqrt 3 }}{6} = \frac{{a\sqrt 3 .\sqrt 3 }}{6} = \frac{a}{2}\).
Vì AC = CE = AE = BF = FD = BD nên ta có ∆ACE = ∆BFD (c.c.c).
Do đó bán kính đường tròn nội tiếp tương ứng của ∆ACE và ∆BFD bằng nhau, và bằng \(\frac{a}{2}\).