Giải bài 32 trang 116 sách bài tập toán 9 - Cánh diều tập 1 — Không quảng cáo

Đề bài

Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M.

a) Tính số đo cung nhỏ AB và số đo cung lớn AB nếu $\widehat {AMB} = 40^\circ$.

b) Tính diện tích của tứ giác OAMB theo R nếu số đo cung nhỏ AB bằng 120⁰.

Lời giải chi tiết

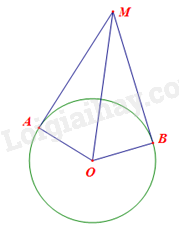
a) Do MA, MB là 2 tiếp tuyến của (O) nên $MA \bot OA,MB \bot OB$, hay $\widehat A = \widehat B = 90^\circ$.

Xét tứ giác OAMB có $\widehat A + \widehat {AOB} + \widehat B + \widehat {AMB} = 360^\circ$, do đó

$\widehat {AOB} = 360^\circ  - \left( {\widehat A + \widehat B + \widehat {AMB}} \right) \\= 360^\circ  - \left( {90^\circ  + 90^\circ  + 40^\circ } \right) = 140^\circ .$

Ta có số đo cung nhỏ AB bằng số đo góc ở tâm $\widehat {AOB}$, bằng $140^\circ$;

Số đo cung lớn AB là $360^\circ  - 140^\circ  = 220^\circ$.

b) Số đo cung nhỏ AB là 120⁰ nên $\widehat {AOB} = 120^\circ$.

Do MA, MB là 2 tiếp tuyến của (O) nên OA là tia phân giác của góc AOB,

do đó $\widehat {AOM} = \widehat {BOM} = \frac{{\widehat {AOB}}}{2} = \frac{{120^\circ }}{2} = 60^\circ$.

Xét tam giác OMA vuông tại A, ta có

$MA = AO.\tan \widehat {AOM} = R.\tan 60^\circ  = R\sqrt 3$

Diện tích tam giác OMA là

${S_{OMA}} = \frac{1}{2}MA.AO = \frac{1}{2}R\sqrt 3 .R = \frac{{\sqrt 3 {R^2}}}{2}$.

Xét tam giác OMB vuông tại B, ta có

$MB = BO.\tan \widehat {BOM} = R.\tan 60^\circ  = R\sqrt 3$.

Diện tích tam giác OMB là

${S_{OMB}} = \frac{1}{2}MB.BO = \frac{1}{2}R\sqrt 3 .R = \frac{{\sqrt 3 {R^2}}}{2}$.

Diện tích AMBO là:

${S_{AMBO}} = {S_{OMA}} + {S_{OMB}} = \frac{{\sqrt 3 {R^2}}}{2} + \frac{{\sqrt 3 {R^2}}}{2} = \sqrt 3 {R^2}$.