Giải bài 38 trang 136 sách bài tập toán 9 - Cánh diều tập 2
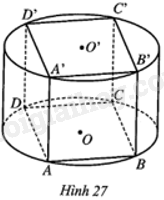
Cho hình lập phương ABCD.A’B’C’D’ có thể tích bằng 27a3. Hình trụ (T) có hai đáy là hai đường tròn (O), (O’) lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’ (Hình 27). Tính diện tích toàn phần của hình trụ (T) theo a.
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ có thể tích bằng 27a 3 . Hình trụ (T) có hai đáy là hai đường tròn (O), (O’) lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’ (Hình 27). Tính diện tích toàn phần của hình trụ (T) theo a.
Phương pháp giải - Xem chi tiết
Dựa vào: Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r(h + r)\) .
Lời giải chi tiết
Do hình lập phương ABCD.A’B’C’D’ có thể tích bằng 27a 3 nên cạnh hình lập phương là \(\sqrt[3]{{27{a^3}}} = 3a\).
Suy ra cạnh của hình vuông ABCD là 3a và bán kính của hình trụ bằng bán kính của đường tròn (O) ngoại tiếp hình vuông ABCD và bằng \(\frac{{3a\sqrt 2 }}{2}\).
Vậy diện tích toàn phần của hình trụ (T) là:
\(2\pi .\frac{{3a\sqrt 2 }}{2}.3a + 2\pi .{\left( {\frac{{3a\sqrt 2 }}{2}} \right)^2} = 9\pi {a^2}(\sqrt 2 + 1)\)