Giải bài 4.18 trang 48 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cosC theo hai cách và suy ra (A{C^2} = BC.HC).
Đề bài
Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cosC theo hai cách và suy ra \(A{C^2} = BC.HC\).
Phương pháp giải - Xem chi tiết
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
Lời giải chi tiết
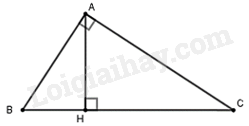
Tam giác ABC vuông tại A nên \(\cos C = \frac{{AC}}{{BC}}\).
Tam giác AHC vuông tại H nên \(\cos C = \frac{{HC}}{{AC}}\).
Do đó, \(\frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}\) nên \(A{C^2} = BC.HC\).
Cùng chủ đề:
Giải bài 4. 18 trang 48 sách bài tập toán 9 - Kết nối tri thức tập 1