Giải bài 4.59 trang 69 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
Cho hình bình hành ABCD tâm O. Gọi M,N theo thứ tự là trung điểm của BC,AD. Gọi I,J lần lượt là giao điểm của BD với AM,CN. Xét các cevtơ khác \overrightarrow 0 , các đầu mút lấy từ các điểm A,B,C,D,M,N,I,J,O.
Đề bài
Cho hình bình hành \(ABCD\) tâm \(O.\) Gọi \(M,\,\,N\) theo thứ tự là trung điểm của \(BC,\,\,AD.\) Gọi \(I,\,\,J\) lần lượt là giao điểm của \(BD\) với \(AM,\,\,CN.\) Xét các cevtơ khác \(\overrightarrow 0 ,\) các đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,M,\,\,N,\,\,I,\,\,J,\,\,O.\)
a) Hãy chỉ ra những vectơ bằng vectơ \(\overrightarrow {AB} ;\) những vectơ cùng hướng với \(\overrightarrow {AB} .\)
b) Chứng minh ằng \(BI = IJ = JD.\)
Lời giải chi tiết
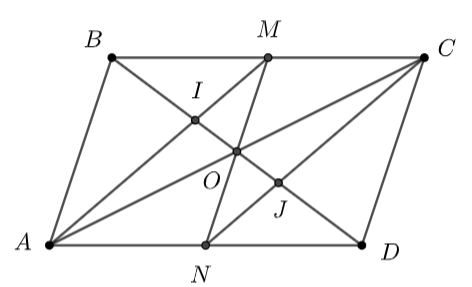
a) Các vectơ bằng vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {AB} ,\,\,\overrightarrow {NM} ,\,\,\overrightarrow {CD} \)
Các vectơ cùng hướng với \(\overrightarrow {AB} \) là: \(\overrightarrow {AB} ,\,\,\overrightarrow {NO} ,\,\,\overrightarrow {OM} ,\,\,\overrightarrow {CD} \)
b) Ta có: \(I\) là trọng tâm của \(\Delta ABC\)
\( \Rightarrow \) \(\overrightarrow {BI} = \frac{2}{3}\overrightarrow {BO} = \frac{2}{3}.\frac{1}{2}\overrightarrow {BD} = \frac{1}{3}\overrightarrow {BD} \) (1)
Ta có: \(J\) là trọng tâm của \(\Delta ACD\)
\( \Rightarrow \) \(\overrightarrow {JD} = \frac{2}{3}\overrightarrow {OD} = \frac{2}{3}.\frac{1}{2}\overrightarrow {BD} = \frac{1}{3}\overrightarrow {BD} \) (2)
Ta có: \(\overrightarrow {BD} = \overrightarrow {BI} + \overrightarrow {IJ} + \overrightarrow {JD} \)
\( \Rightarrow \) \(\overrightarrow {IJ} = \overrightarrow {BD} - \overrightarrow {BI} - \overrightarrow {JD} = \overrightarrow {BD} - \frac{1}{3}\overrightarrow {BD} - \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\overrightarrow {BD} \) (3)
Từ (1), (2) và (3) \( \Rightarrow \) \(\overrightarrow {BI} = \overrightarrow {IJ} = \overrightarrow {JD} \) \( \Rightarrow \) \(BI = IJ = JD\)