Giải bài 4.64 trang 70 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
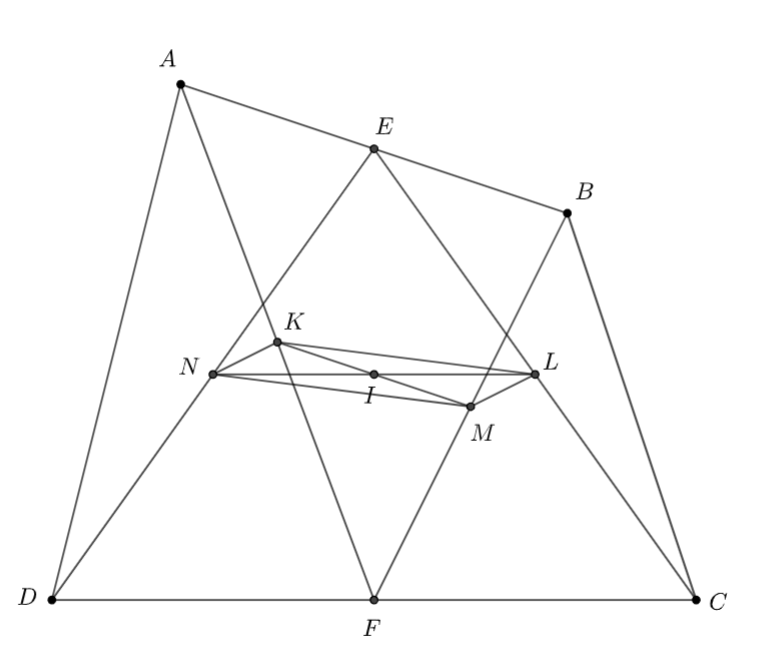
Cho tứ giác lồi ABCD, không có hai cạnh nào song song. Gọi E,F theo thứ tự là trung điểm của AB,CD. Gọi K,L,M,N lần lượt là trung điểm của AF,CE,BF,DE.
Đề bài
Cho tứ giác lồi \(ABCD,\) không có hai cạnh nào song song. Gọi \(E,\,\,F\) theo thứ tự là trung điểm của \(AB,\,\,CD.\) Gọi \(K,\,\,L,\,\,M,\,\,N\) lần lượt là trung điểm của \(AF,\,\,CE,\,\,BF,\,\,DE.\)
a) Chứng minh rằng tứ giác \(KLMN\) là một hình bình hành.
b) Gọi \(I\) là giao điểm của \(KM,\,\,LN.\) Chứng minh rằng \(E,\,\,I,\,\,F\) thẳng hàng.
Lời giải chi tiết
a) Ta có: \(\overrightarrow {AE} + \overrightarrow {FC} = \left( {\overrightarrow {AK} + \overrightarrow {KL} + \overrightarrow {LE} } \right) + \left( {\overrightarrow {FK} + \overrightarrow {KL} + \overrightarrow {LC} } \right)\)
\( = 2\overrightarrow {KL} + \left( {\overrightarrow {AK} + \overrightarrow {FK} } \right) + \left( {\overrightarrow {LE} + \overrightarrow {LC} } \right)\)
\( = 2\overrightarrow {KL} \) (1)
Ta có: \(\overrightarrow {EB} + \overrightarrow {DF} = \left( {\overrightarrow {EN} + \overrightarrow {NM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {NM} + \overrightarrow {MF} } \right)\)
\( = 2\overrightarrow {NM} + \left( {\overrightarrow {EN} + \overrightarrow {DN} } \right) + \left( {\overrightarrow {MB} + \overrightarrow {MF} } \right)\)
\( = 2\overrightarrow {NM} \) (2)
Ta có: \(\overrightarrow {AE} + \overrightarrow {FC} = \overrightarrow {EB} + \overrightarrow {DF} \) (3)
Từ (1), (2) và (3) \( \Rightarrow \) \(\overrightarrow {KL} = \overrightarrow {NM} \)
\( \Rightarrow \) tứ giác \(MNKL\) là hình bình hành.
b) Gọi \(I\) là giao điểm của \(KM,\,\,LN.\)
Ta có: \(\overrightarrow {EI} = \frac{1}{2}\left( {\overrightarrow {EN} + \overrightarrow {EL} } \right) = \frac{1}{2}\left( {\frac{1}{2}\overrightarrow {ED} + \frac{1}{2}\overrightarrow {EC} } \right)\)
\(\begin{array}{l} = \frac{1}{4}\left( {\overrightarrow {ED} + \overrightarrow {EC} } \right) = \frac{1}{4}.2\overrightarrow {EF} \\ = \frac{1}{2}\overrightarrow {EF} \end{array}\)
\( \Rightarrow \) \(\overrightarrow {EI} \) và \(\overrightarrow {EF} \) cùng hướng
\( \Rightarrow \) ba điểm \(E,\,\,I,\,\,F\) thẳng hàng