Giải bài 4. 63 trang 70 sách bài tập toán 10 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho tam giác $ABC$ với trọng tâm $G.$ Lấy điểm $A',\,\,B'$ sao cho $\overrightarrow {AA'}  = 2\overrightarrow {BC} ,\,\,\overrightarrow {BB'}  = 2\overrightarrow {CA} .$ Gọi $G'$ là trọng tâm của tam giác $A'B'C.$ Chứng minh rằng $GG'$ song song với $AB.$

Lời giải chi tiết

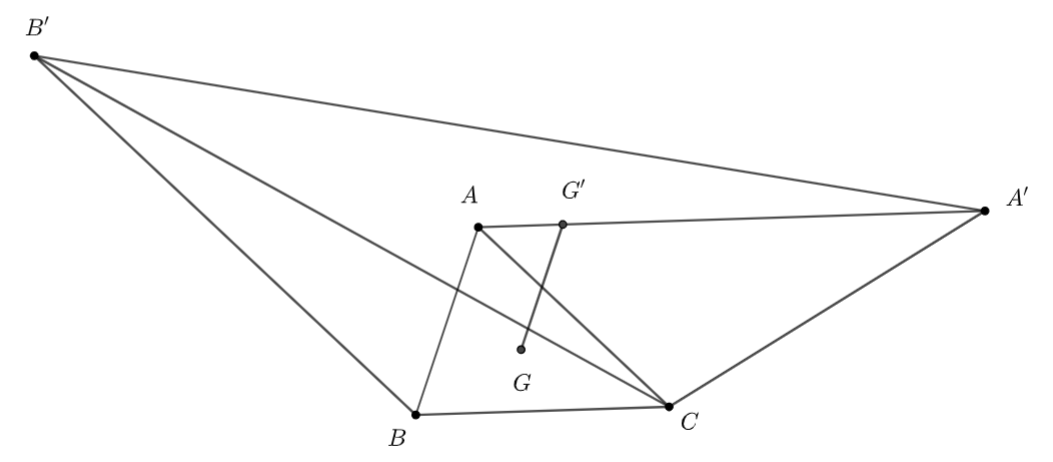
Ta có: $G$ và $G'$ lần lượt là trọng tâm của $\Delta ABC$ và $\Delta A'B'C$

$\Rightarrow$ $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$ và $\overrightarrow {G'A'}  + \overrightarrow {G'B'}  + \overrightarrow {G'C}  = \overrightarrow 0$

Ta có: $\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC}  = 3\overrightarrow {GG'}$

$\begin{array}{l} \Leftrightarrow \,\,2\overrightarrow {BC}  + 2\overrightarrow {CA}  = 3\overrightarrow {GG'} \\ \Leftrightarrow \,\,2\overrightarrow {BA}  = 3\overrightarrow {GG'} \end{array}$

$\Rightarrow$ $AB$//$GG'$ (đpcm)