Giải bài 4. 8 trang 45 sách bài tập toán 9 - Kết nối tri thức tập 1 — Không quảng cáo

Đề bài

Vẽ góc $\alpha$ trong mỗi trường hợp:

a) $\cos \alpha  = 0,4$;

b) $\tan \alpha  = \frac{2}{3}$;

c) $\cot \alpha  = \frac{3}{4}$.

Lời giải chi tiết

a) $\cos \alpha  = 0,4 = \frac{2}{5}$

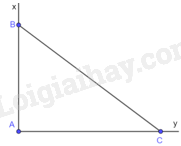
+ Vẽ góc vuông xAy, lấy điểm B thuộc tia Ax sao cho $AB = 2cm$.

+ Vẽ đường tròn tâm B, bán kính 5cm, đường tròn này cắt tia Ay tại C.

+ Khi đó ta được tam giác ABC vuông tại A, $AB = 2cm$, $BC = 5cm$ nên $\cos \widehat {ABC} = \frac{{AB}}{{BC}} = \frac{2}{5}$.

Vậy góc ABC vẽ như trên thỏa mãn yêu cầu bài toán.

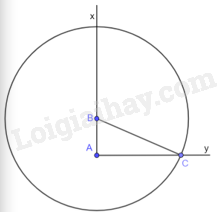
b) + Vẽ góc vuông xAy, lấy điểm B thuộc tia Ax sao cho $AB = 3cm$.

+ Lấy điểm C thuộc tia Ay sao cho $AC = 2cm$.

+ Khi đó ta được tam giác ABC vuông tại A, $AB = 3cm$, $AC = 2cm$ nên $\tan \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{2}{3}$.

Vậy góc ABC vẽ như trên thỏa mãn yêu cầu bài toán.

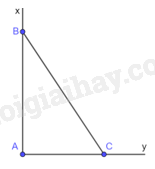
c) + Vẽ góc vuông xAy, lấy điểm B thuộc tia Ax sao cho $AB = 3cm$.

+ Lấy điểm C thuộc tia Ay sao cho $AC = 4cm$.

+ Khi đó ta được tam giác ABC vuông tại A, $AB = 3cm$, $AC = 4cm$ nên $\cot \widehat {ABC} = \frac{{AB}}{{AC}} = \frac{3}{4}$.

Vậy góc ABC vẽ như trên thỏa mãn yêu cầu bài toán.