Giải bài 4 trang 109 vở thực hành Toán 9 — Không quảng cáo

Đề bài

Cho đường tròn (O; 5cm).

a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5cm.

b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).

c) Tính số đo và độ dài của cung nhỏ AB.

d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.

Lời giải chi tiết

a) Vẽ dây AB cách O một khoảng 2,5cm:

- Lấy điểm I tùy ý sao cho $OI = 2,5cm$;

- Vẽ đường thẳng vuông góc với OI tại I, cắt (O) tại A và B. Ta có dây AB cần vẽ:

b) (H.5.22)

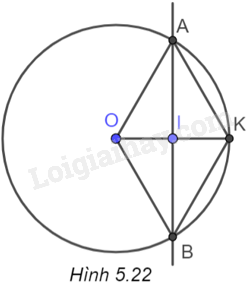
Trong tam giác vuông AOI, ta có $A{I^2} = O{A^2} - O{I^2} = {5^2} - {2,5^2} = 18,75$.

Vậy $AB = 2AI = 2\sqrt {18,75}  \approx 8,66\left( {cm} \right)$

c) (H.5.22)

Kéo dài OI cắt (O) tại K.

Dễ thấy tứ giác AKBO có hai đường chéo AB và OK vuông góc với nhau và cắt nhau tại trung điểm mỗi đường (do $AI = IB$ và $OI = IK = \frac{{OK}}{2}$).

Do đó AKBO là hình thoi.

Từ đó $OA = OK = KA = 5cm$; OAK là tam giác đều, suy ra $\widehat {AOK} = {60^o}$ và $\widehat {AOB} = 2\widehat {AOK} = {120^o}$.

Vậy $sđ\overset\frown{AB}=\widehat{AOK}={{120}^{o}}$.

Độ dài cung nhỏ AB bằng $\frac{{120}}{{180}}\pi .5 = \frac{{10\pi }}{3}\left( {cm} \right)$.

d) Diện tích hình quạt tròn ứng với cung AB là:

${S_q} = \frac{{120}}{{360}}.\pi {.5^2} = \frac{{25\pi }}{3}\left( {c{m^2}} \right)$.