Giải bài 4 trang 99 SGK Toán 10 tập 1 – Cánh diều
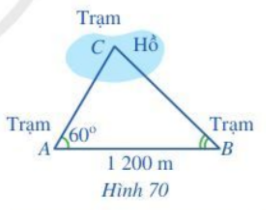
Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và B đến C, người ta làm như sau:
Đề bài
Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và B đến C, người ta làm như sau:
- Đo góc BAC được \({60^o}\), đo góc ABC được \({45^o}\);
- Đo khoảng cách AB được 1 200 m.
Khoảng cách từ trạm C đến các trạm A và B bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải - Xem chi tiết
Tính AB, AC bằng cách áp dụng định lí sin trong tam giác ABC:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Lời giải chi tiết
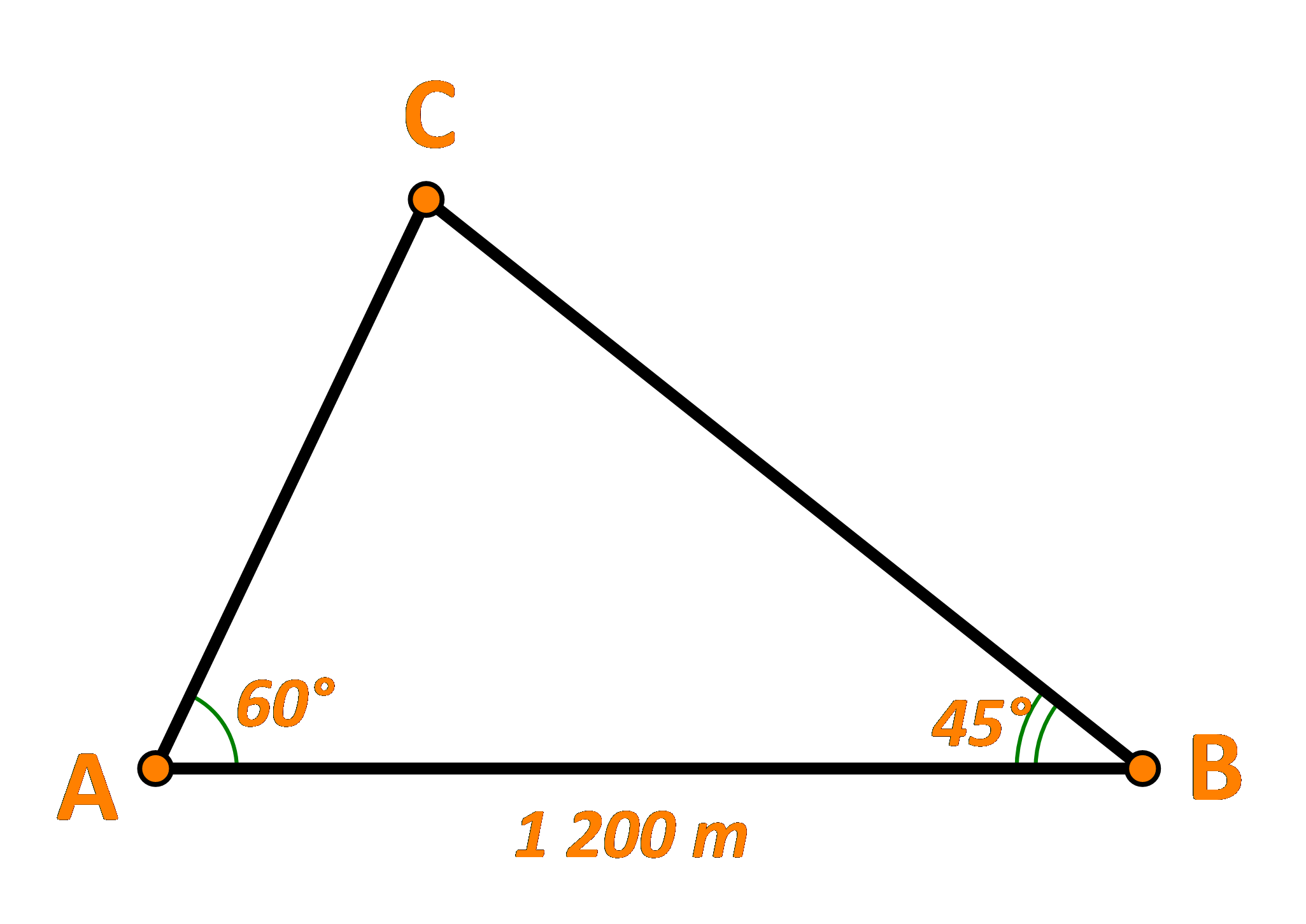
Ta có: \(\widehat C = {180^o} - {60^o} - {45^o} = {75^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \frac{{\sin B.AB}}{{\sin C}}\\BC = \frac{{\sin A.AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \frac{{\sin {{45}^o}.1200}}{{\sin {{75}^o}}} \approx 878\\BC = \frac{{\sin {{60}^o}.1200}}{{\sin {{75}^o}}} \approx 1076\end{array} \right.\)
Vậy AC = 878 m, BC = 1076 m.