Giải Bài 45 trang 83 sách bài tập toán 7 - Cánh diều
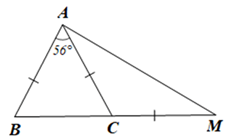
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 56^\circ \). Trên tia đối của tia CB lấy điểm M sao cho AC = CM. Tính số đo mỗi góc của tam giác ABM.
Đề bài
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 56^\circ \). Trên tia đối của tia CB lấy điểm M sao cho AC = CM. Tính số đo mỗi góc của tam giác ABM.
Phương pháp giải - Xem chi tiết
- Sử dụng tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\).
- Tổng ba góc của 1 tam giác bằng \({180^o}\).
- Từ đó tính được số đo các góc của tam giác ABM.
Lời giải chi tiết
• Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\) (hai góc ở đáy).
Xét tam giác ABC có \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \) (tổng ba góc của một tam giác)
Do đó \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 56^\circ }}{2} = 62^\circ \)
• Ta có \(\widehat {ACB} + \widehat {ACM} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {ACM} = 180^\circ - \widehat {ACB} = 180^\circ - 62^\circ = 118^\circ \)
• Vì AC = CM (giả thiết) nên tam giác ACM cân tại C.
Suy ra \(\widehat {CAM} = \widehat {CMA}\) (hai góc ở đáy).
Xét ∆AMC có: \(\widehat {AMC} + \widehat {ACM} + \widehat {MAC} = 180^\circ \) (tổng ba góc của một tam giác).
Do đó \(\widehat {CAM} = \widehat {CMA} = \frac{{180^\circ - \widehat {ACM}}}{2} = \frac{{180^\circ - 118^\circ }}{2} = 31^\circ \)
Ta có \(\widehat {BAM} = \widehat {BAC} + \widehat {CAM} = 56^\circ + 31^\circ = 87^\circ \)
Vậy \(\widehat {BAM} = 87^\circ ,\widehat {ABM} = 62^\circ ,\widehat {AMB} = 31^\circ .\)