Giải bài 5.17 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn (O) và điểm P. a) Giả sử (P in left( O right)). Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P. b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).
Đề bài
Cho đường tròn (O) và điểm P.
a) Giả sử \(P \in \left( O \right)\). Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P.
b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).
Phương pháp giải - Xem chi tiết
a) Vì \(P \in \left( O \right)\) và \(a \bot OP\) tại P nên a là tiếp tuyến của đường tròn (O) tại P.
b) + Gọi I là trung điểm của OP. Suy ra, bốn điểm O, A, P, B thuộc đường tròn tâm I, đường kính OP.
+ Chứng minh tam giác OBP vuông tại B, suy ra \(OB \bot BP\) tại B, suy ra PB là tiếp tuyến của (O) tại B.
+ Chứng minh tam giác OAP vuông tại A, do đó \(OA \bot AP\) tại A, suy ra PA là tiếp tuyến của (O) tại A.
Lời giải chi tiết
a) Vì \(P \in \left( O \right)\) và \(a \bot OP\) tại P nên a là tiếp tuyến của đường tròn (O) tại P.
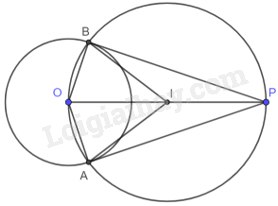
b) Gọi I là trung điểm của OP. Suy ra, bốn điểm O, A, P, B thuộc đường tròn tâm I, đường kính OP.
Tam giác OBP có BI là đường trung tuyến và \(BI = IP = OI = \frac{1}{2}OP\) nên tam giác OBP vuông tại B. Do đó, \(OB \bot BP\) tại B.
Vì B thuộc (O) và \(OB \bot BP\) tại B nên PB là tiếp tuyến của (O) tại B.
Tam giác OAP có AI là đường trung tuyến và \(AI = IP = OI = \frac{1}{2}OP\) nên tam giác OAP vuông tại A. Do đó, \(OA \bot AP\) tại A.
Vì A thuộc (O) và \(OA \bot AP\) tại A nên PA là tiếp tuyến của (O) tại A.