Giải bài 5.28 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho hình thang cân ABCD (AB//CD). a) Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD (từ đó suy ra hai điểm A và B đối xứng với nhau, C và D đối xứng với nhau qua d). b) Giải thích tại sao nếu một đường tròn đi qua ba điểm A, B và C thì nó cũng đi qua điểm D.
Đề bài
Cho hình thang cân ABCD (AB//CD).
a) Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD (từ đó suy ra hai điểm A và B đối xứng với nhau, C và D đối xứng với nhau qua d).
b) Giải thích tại sao nếu một đường tròn đi qua ba điểm A, B và C thì nó cũng đi qua điểm D.
Phương pháp giải - Xem chi tiết
a) - Trường hợp 1: DA cắt CB tại điểm S.
+ Chứng minh tam giác SAB cân tại S và tam giác SDC cân tại S.
+ Do đó, đường trung trực d của AB là đường phân giác của góc ASB và cũng là đường trung trực của DC. Suy ra, A và D lần lượt đối xứng với B và C qua d.
- Trường hợp 2: DA//CB. Khi đó hình thang cân ABCD là hình chữ nhật. Do đó, A và D lần lượt đối xứng với B và C qua d.
b) + Giả sử O là tâm của đường tròn đi qua ba điểm A, B, C.
+ Chứng minh đường trung trực d của AB đi qua O, suy ra d là trục đối xứng của đường tròn (O).
+ Vì D đối xứng với C qua d, mà \(C \in \left( O \right)\) nên \(D \in \left( O \right)\), hay (O) đi qua D.
Lời giải chi tiết
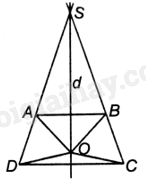
a) Trường hợp 1: DA cắt CB tại điểm S.
Vì ABCD là hình thang cân nên \(\widehat {SAB} = \widehat {SBA} = \widehat {SDC} = \widehat {SCD}\), suy ra tam giác SAB cân tại S và tam giác SDC cân tại S.
Do đó, đường trung trực d của AB là đường phân giác của góc ASB và cũng là đường trung trực của DC.
Suy ra, A và D lần lượt đối xứng với B và C qua d.
Trường hợp 2: DA//CB.
Khi đó hình thang cân ABCD là hình chữ nhật.
Do đó, A và D lần lượt đối xứng với B và C qua d.
b) Giả sử O là tâm của đường tròn đi qua ba điểm A, B, C.
Khi đó, đường trung trực d của AB đi qua O (vì \(OA = OB\)).
Do đó, d là trục đối xứng của đường tròn (O).
Theo câu a, D đối xứng với C qua d, mà \(C \in \left( O \right)\) nên \(D \in \left( O \right)\), hay (O) đi qua D.