Giải bài 5.32 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Từ B và từ C kẻ hai đường thẳng tiếp xúc với đường tròn (A; AH) lần lượt tại D và E. Chứng minh rằng: a) Hai điểm D và E đối xứng với nhau qua A; b) DE tiếp xúc với đường tròn đường kính BC.
Đề bài
Cho tam giác ABC vuông tại A, đường cao AH. Từ B và từ C kẻ hai đường thẳng tiếp xúc với đường tròn (A; AH) lần lượt tại D và E. Chứng minh rằng:
a) Hai điểm D và E đối xứng với nhau qua A;
b) DE tiếp xúc với đường tròn đường kính BC.
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(\widehat {DAH} = 2\widehat {BAH}\), \(\widehat {HAE} = 2\widehat {HAC}\), \(\widehat {BAH} + \widehat {HAC} = {90^o}\) suy ra \(\widehat {DAH} + \widehat {HAE} = {180^o}\)
Do đó, ba điểm D, A, E thẳng hàng.
+ Vì D, E thuộc (A; AH) nên \(AE = AD\). Do đó, D và E đối xứng với nhau qua A.
b) + Gọi O là trung điểm của BC.
+ Chứng minh A thuộc đường tròn tâm O, đường kính BC.
+ Chứng minh \(\widehat {HBA} = \widehat {HAC}\), \(\widehat {HAC} = \widehat {CAE}\) nên \(\widehat {HBA} = \widehat {CAE}\).
+ Chứng minh \(\widehat {{C_1}} = \widehat {{A_1}}\).
+ Chứng minh \(\widehat {{B_1}} + \widehat {{C_1}} = {90^o}\), suy ra \(\widehat {{A_2}} + \widehat {{A_1}} = {90^o}\) hay \(\widehat {OAE} = {90^o}\), suy ra \(DE \bot OA\) tại A, suy ra, DE tiếp xúc với đường tròn đường kính BC tại A.
Lời giải chi tiết
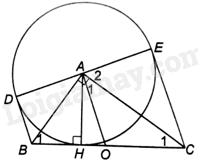
a) Vì \(BC \bot AH\) tại H nên BC là tiếp tuyến của (A), mà BD là tiếp tuyến của (A) nên AB là phân giác của góc DAH, suy ra \(\widehat {DAH} = 2\widehat {BAH} = 2\widehat {DAB}\).
Chứng minh tương tự ta có: \(\widehat {HAE} = 2\widehat {HAC} = 2\widehat {CAE}\).
Tam giác ABC vuông tại A nên \(\widehat {BAH} + \widehat {HAC} = {90^o}\).
Ta có: \(\widehat {DAH} + \widehat {HAE} = 2\widehat {BAH} + 2\widehat {HAC} \\= 2\left( {\widehat {BAH} + \widehat {HAC}} \right) = {2.90^o} = {180^o}\)
Do đó, ba điểm D, A, E thẳng hàng.
Vì D, E thuộc (A; AH) nên \(AE = AD\). Do đó, D và E đối xứng với nhau qua A.
b) Gọi O là trung điểm của BC.
Tam giác ABC vuông tại A có AO là đường trung tuyến nên \(AO = OB = OC\). Do đó, A thuộc đường tròn tâm O, đường kính BC.
Ta có:
\(\widehat {HBA} + \widehat {{C_1}} = \widehat {{C_1}} + \widehat {HAC}\left( { = {{90}^o}} \right)\) nên \(\widehat {HBA} = \widehat {HAC}\).
Mà \(\widehat {HAC} = \widehat {CAE}\) nên \(\widehat {HBA} = \widehat {CAE}\)
Vì \(AO = OC\) nên tam giác AOC cân tại O, suy ra \(\widehat {{C_1}} = \widehat {{A_1}}\)
Tam giác ABC vuông tại A nên \(\widehat {{B_1}} + \widehat {{C_1}} = {90^o}\), suy ra \(\widehat {{A_2}} + \widehat {{A_1}} = {90^o}\) hay \(\widehat {OAE} = {90^o}\).
Do đó, \(DE \bot OA\) tại A.
Do đó, DE tiếp xúc với đường tròn đường kính BC tại A.