Giải bài 5. 35 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1 — Không quảng cáo

Đề bài

Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B.

a) Chứng minh rằng MA và MB là hai tiếp tuyến của (N).

b) Đường thẳng qua N và vuông góc với NA cắt MB tại C. Chứng minh hai điểm M và N đối xứng với nhau qua OC.

c) Đường thẳng qua M và vuông góc với MA cắt NB tại D. Chứng minh ba điểm O, C và D thẳng hàng.

Lời giải chi tiết

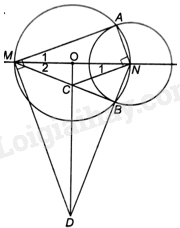
a) Vì M, A, N, B thuộc (O) nên $OA = OB = OM = ON$.

Tam giác MAN có $OA = OM = ON = \frac{1}{2}MN$, tức là trung tuyến OA có độ dài bằng nửa độ dài cạnh MN nên tam giác MAN vuông tại A.

Do đó, $MA \bot AN$ tại A.

Mà A thuộc (N) nên MA là tiếp tuyến của (N).

Tam giác MBN có $OB = OM = ON = \frac{1}{2}MN$, tức là trung tuyến OB có độ dài bằng nửa độ dài cạnh MN nên tam giác MBN vuông tại B.

Do đó, $MB \bot BN$ tại B.

Mà B thuộc (N) nên MB là tiếp tuyến của (N).

b) Vì AM//NC (cùng vuông góc với AN) nên $\widehat {{M_1}} = \widehat {{N_1}}$.

Vì MA và MB là hai tiếp tuyến cắt nhau của (N) nên MN là phân giác của góc AMB.

Do đó, $\widehat {{M_1}} = \widehat {{M_2}}$.

Do đó, $\widehat {{M_2}} = \widehat {{N_1}}$.

Suy ra, tam giác CMN cân tại C.

Do đó, trung tuyến CO (vì $OM = ON$) đồng thời là đường trung trực của MN.

Do đó, hai điểm M và N đối xứng với nhau qua OC.

c) Vì $MA \bot MD$ và MD//AC (cùng vuông góc với MA) nên $\widehat {DMN} = \widehat {ANM}$.

Vì MA và MB là hai tiếp tuyến cắt nhau của (N) nên NM là phân giác của góc ANB.

Do đó, $\widehat {DNM} = \widehat {ANM}$

Do đó, $\widehat {DMN} = \widehat {DNM}$ nên tam giác DMN cân tại D, suy ra D nằm trên đường trung trực CO của MN.

Vậy ba điểm O, C và D thẳng hàng.