Giải bài 5 trang 107 sách bài tập toán 9 - Cánh diều tập 2
Cho ngũ giác ABCDE. Chứng minh: AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Đề bài
Cho ngũ giác ABCDE. Chứng minh:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Phương pháp giải - Xem chi tiết
Áp dụng bất đẳng thức trong tam giác là một định lý phát biểu rằng trong một tam giác, chiều dài của một cạnh phải nhỏ hơn tổng, nhưng lớn hơn hiệu của hai cạnh còn lại.
Lời giải chi tiết
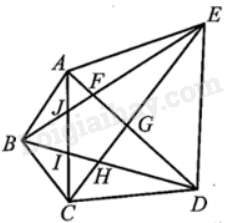
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.