Giải bài 5 trang 21 sách bài tập toán 12 - Chân trời sáng tạo
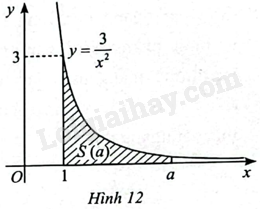
Kí hiệu (Sleft( a right)) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số (y = frac{3}{{{x^2}}}), trục hoành và hai đường thẳng (x = 1,x = a) với (a > 1) (Hình 12). Tính giới hạn (mathop {lim }limits_{a to + infty } Sleft( a right)).
Đề bài
Kí hiệu \(S\left( a \right)\) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \frac{3}{{{x^2}}}\), trục hoành và hai đường thẳng \(x = 1,x = a\) với \(a > 1\) (Hình 12). Tính giới hạn \(\mathop {\lim }\limits_{a \to + \infty } S\left( a \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết
Ta có:
\(\begin{array}{l}S\left( a \right) = \int\limits_1^a {\left| {\frac{3}{{{x^2}}}} \right|dx} = \int\limits_1^a {\frac{3}{{{x^2}}}dx} = \left. {\left( { - \frac{3}{x}} \right)} \right|_1^a = 3 - \frac{3}{a}\\\mathop {\lim }\limits_{a \to + \infty } S\left( a \right) = \mathop {\lim }\limits_{a \to + \infty } \left( {3 - \frac{3}{a}} \right) = 3\end{array}\).