Giải bài 5 trang 25 sách bài tập toán 12 - Chân trời sáng tạo — Không quảng cáo

Đề bài

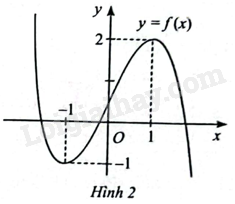
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Biết rằng đạo hàm \(f'\left( x \right)\) liên tục trên \(\mathbb{R}\). Tính \(\int\limits_{ - 1}^1 {f'\left( x \right)dx} \).

Lời giải chi tiết

Dựa vào đồ thị hàm số ta có: \(f\left( { - 1} \right) =  - 1,f\left( 1 \right) = 2\).

\(\int\limits_{ - 1}^1 {f'\left( x \right)dx}  = f\left( 1 \right) = f\left( { - 1} \right) = 2 - \left( { - 1} \right) = 3\).