Giải bài 5 trang 45 vở thực hành Toán 8
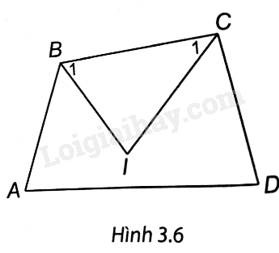
Cho tứ giác ABCD có \(\widehat A = {70^0},\widehat D = {80^0}.\)
Đề bài
Cho tứ giác ABCD có \(\widehat A = {70^0},\widehat D = {80^0}.\)
a) Tính \(\widehat {ABC} + \widehat {BCD}\).
b) Biết các tia phân giác của các góc B và C cắt nhau tại I. Tính số đo \(\widehat {BIC}\).
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí tổng các góc của tứ giác: Tổng các góc của một tứ giác bằng \({360^0}\) .
b) Sử dụng định lí tổng các góc của tam giác: Tổng các góc của một tam giác bằng \({180^0}\) .
Lời giải chi tiết
a) Vì tổng các góc của tứ giác \({\rm{ABCD}}\) bằng \({360^0}\) nên ta có:
\(\widehat {{\rm{DAB}}}{\rm{ + }}\widehat {{\rm{CDA}}}{\rm{ + }}\widehat {{\rm{ABC}}}{\rm{ + }}\widehat {{\rm{BCD}}}{\rm{ = 36}}{{\rm{0}}^{\rm{0}}}\) nên
\(\widehat {{\rm{ABC}}} + \widehat {{\rm{BCD}}} = {360^0} - \widehat {{\rm{DAB}}} - \widehat {{\rm{CDA}}} = {360^0} - {70^0} - {80^0} = {210^0}\) .
b) Vì \({\rm{BI}},{\rm{CI}}\) lần lượt là tia phân giác của góc \({\rm{ABC}}\) và góc \({\rm{BCD}}\) nên
\({\widehat {\rm{B}}_{\rm{1}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}\widehat {{\rm{ABC}}}{\rm{,}}{\widehat {\rm{C}}_{\rm{1}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}\widehat {{\rm{BCD}}}\)
Do đó \({\widehat {\rm{B}}_{\rm{1}}}{\rm{ + }}{\widehat {\rm{C}}_{\rm{1}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}\widehat {{\rm{ABC}}}{\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}}\widehat {{\rm{BCD}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{(}}\widehat {{\rm{ABC}}}{\rm{ + }}\widehat {{\rm{BCD}}}{\rm{) = 10}}{{\rm{5}}^{\rm{0}}}\) .
Áp dụng định lí tổng ba góc trong tam giác BIC có:
\(\widehat {{\rm{BIC}}} + {\widehat {\rm{B}}_1} + {\widehat {\rm{C}}_1} = {180^0} \Rightarrow \widehat {{\rm{BIC}}} = {180^0} - \left( {{{\widehat {\rm{B}}}_1} + {{\widehat {\rm{C}}}_1}} \right) = {75^0}\)
Vậy \(\widehat {{\rm{BIC}}} = {75^0}\) .