Giải bài 5 trang 8 vở thực hành Toán 9 tập 2
Biết đường cong trong hình bên là một parabol (y = a{x^2}). a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc parabol có hoành độ (x = - 2). c) Tìm các điểm thuộc parabol có tung độ (y = 8).
Đề bài
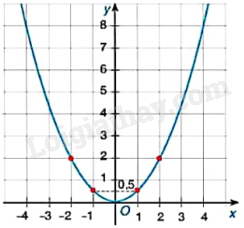
Biết đường cong trong hình bên là một parabol \(y = a{x^2}\).
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = - 2\).
c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).
Phương pháp giải - Xem chi tiết
a) Đồ thị hàm số đi qua điểm (2; 2) nên nên thay tọa độ điểm (2; 2) vào hàm số \(y = a{x^2}\) ta tìm được a.
b) Thay \(x = - 2\) vào hàm số \(y = 0,5{x^2}\) để tìm tung độ y.
c) Thay \(y = 8\) vào hàm số \(y = 0,5{x^2}\) để tìm hoành độ x.
Lời giải chi tiết
a) Đồ thị của hàm số đi qua điểm (2; 2) nên: \(a{.2^2} = 2\) hay \(a = \frac{1}{2}\).
Do đó, parabol đã cho là đồ thị của hàm số \(y = \frac{1}{2}{x^2}\).
b) Thay \(x = - 2\) ta được: \(y = \frac{1}{2}.{\left( { - 2} \right)^2} = 2\).
Vậy tung độ của điểm thuộc parabol có hoành độ \(x = - 2\) là \(y = 2\).
c) Ta có \(y = 8\) nên \(\frac{1}{2}{x^2} = 8\) hay \({x^2} = 16\). Suy ra \(x = 4\) hoặc \(x = - 4\).
Vậy có hai điểm cần tìm là \(\left( { - 4;8} \right)\) và \(\left( {4;8} \right)\).