Giải bài 55 trang 63 SBT toán 10 - Cánh diều
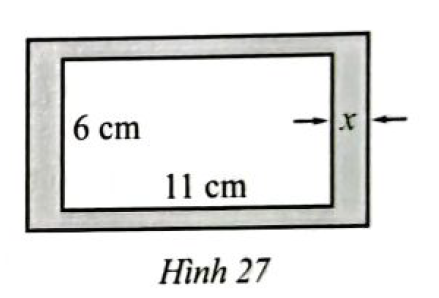
Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6 cm x 11 cm, độ rộng viền xung quanh là \(x\) cm (Hình 27).
Đề bài
Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6 cm x 11 cm, độ rộng viền xung quanh là \(x\) cm (Hình 27). Diện tích của viền khung ảnh không vượt quá \(38c{m^2}\). Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu cm?
Phương pháp giải - Xem chi tiết
Đặt độ rộng của viền khung ảnh là \(x\)(cm) (\(x > 0\)). Biểu diễn diện tích viền khung ảnh và giải bất phương trình
Lời giải chi tiết
Đặt độ rộng của viền khung ảnh là \(x\)(cm) (\(x > 0\)).
Ta có diện tích viền khung ảnh là \(\left( {11 + 2x} \right)\left( {6 + 2x} \right) - 66 = 4{x^2} + 34x\) (\(c{m^2}\))
Theo đề bài ta có: \(4{x^2} + 34x \le 38 \Leftrightarrow 4{x^2} + 34x - 38 \le 0\)
Tam thức bậc hai \(4{x^2} + 34x - 38\) có hai nghiệm \({x_1} = \frac{{ - 19}}{2};{x_2} = 1\) và có hệ số \(a = 4 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(4{x^2} + 34x - 38\) mang dấu “-” là \(\left[ {\frac{{ - 19}}{2};1} \right]\)
Do đó \(0 < x \le 1\)
Vậy độ rộng viền khung ảnh lớn nhất là 1 cm.