Giải bài 56 trang 118 sách bài tập toán 11 - Cánh diều
Cho mặt phẳng \(\left( P \right)\), ba điểm \(A\), \(B\), \(C\) không thẳng hàng và không nằm trên \(\left( P \right)\).
Đề bài
Cho mặt phẳng \(\left( P \right)\), ba điểm \(A\), \(B\), \(C\) không thẳng hàng và không nằm trên \(\left( P \right)\). Chứng minh rằng nếu ba đường thẳng \(AB\), \(BC\), \(CA\) cắt mặt phẳng \(\left( P \right)\) lần lượt tại các điểm \(M\), \(N\), \(P\) thì \(M\), \(N\), \(P\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Chứng minh rằng 3 điểm \(M\), \(N\), \(P\) cùng thuộc giao tuyến của \(\left( P \right)\) và \(\left( {ABC} \right)\).
Lời giải chi tiết
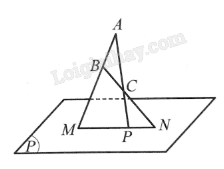
Do ba điểm \(A\), \(B\), \(C\) không thẳng hàng, nên tồn tại một mặt phẳng \(\left( Q \right)\) đi qua 3 điểm này.
Vì \(M \in AB\), mà \(AB \subset \left( Q \right)\) nên \(M \in \left( Q \right)\). Mặt khác, do \(M \in \left( P \right)\) nên hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung. Từ đó ta suy ra tồn tại giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\), và \(M\) nằm trên giao tuyến này.
Chứng minh tương tự, ta cũng suy ra \(N\) và \(P\) cũng nằm trên giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Do đó, ba điểm \(M\), \(N\), \(P\) thẳng hàng.
Bài toán được chứng minh.