Giải bài 58 trang 119 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Trong các khẳng định sau, có bao nhiêu khẳng định đúng?

(1): Trong không gian, hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau,

(2): Trong không gian, hai đường thẳng vuông góc với nhau thì cùng nằm trên một mặt phẳng.

(3): Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

(4): Đường thẳng song song với một trong hai mặt phẳng vuông góc thì song song hoặc nằm trên mặt phẳng còn lại.

(5): Ba mặt phẳng đôi một vuông góc với nhau thì ba giao tuyến tạo thành cũng đôi một vuông góc với nhau.

A. 2

B. 3

C. 4

D. 5

Lời giải chi tiết

Khẳng định 1 là sai. Xét hình lập phương \(ABCD.A'B'C'D'\). Ta có \(AD\) và \(A'B'\) cùng vuông góc với \(AA'\), nhưng \(AD\) và \(A'B'\) không cùng nằm trong mặt phẳng nào cả.

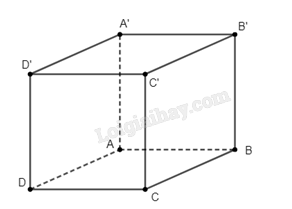
Khẳng định 2 là sai. Xét hình lập phương \(ABCD.A'B'C'D'\), ta thấy rằng \(BB'\) vuông góc với \(CD\), nhưng \(BB'\) và \(CD\) không cùng nằm trong mặt phẳng nào cả.

Khẳng định 3 là đúng, do theo tính chất, đường thẳng vuông góc với mặt phẳng thì nó sẽ vuông góc với tất cả các đường thẳng nằm trong mặt phẳng đó.

Khẳng định 4 là sai. Xét hình lập phương \(ABCD.A'B'C'D'\), ta thấy rằng hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {BCC'B'} \right)\) vuông góc với nhau, đường thẳng \(A'B'\) song song với \(\left( {ABCD} \right)\), nhưng \(A'B'\) không song song hay nằm trong mặt phẳng \(\left( {BCC'B'} \right)\).

Khẳng định 5 là đúng. Xét ba mặt phẳng \(\left( P \right)\), \(\left( Q \right)\) và \(\left( R \right)\) đôi một vuông góc với nhau. Gọi \(a\), \(b\), \(c\) lần lượt là giao tuyến của các cặp mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\), \(\left( Q \right)\) và \(\left( R \right)\), \(\left( R \right)\) và \(\left( P \right)\).

Do \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với \(\left( R \right)\), nên giao tuyến \(a\) của \(\left( P \right)\) và \(\left( Q \right)\) cũng vuông góc với \(\left( R \right)\). Mà \(b\) và \(c\) cũng nằm trên \(\left( R \right)\) nên \(a\) vuông góc với \(b\) và \(a\) vuông góc với \(c\). Tương tự ta cũng suy ra \(b\) vuông góc với \(c\), tức là \(a\), \(b\), \(c\) đôi một vuông góc với nhau.

Đáp án đúng là A.