Giải bài 6. 21 trang 47 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

Thống kê về số vật nuôi trong 98 hộ gia đình ta có kết quả sau:

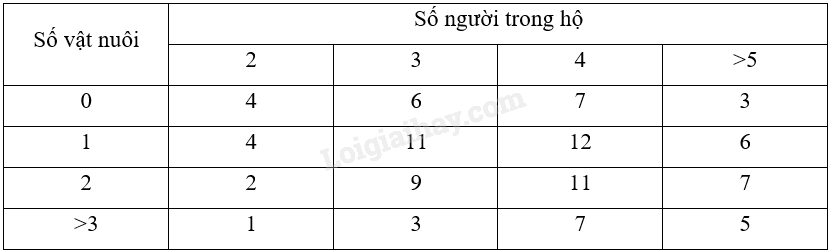
Chọn ngẫu nhiên một hộ gia đình. Tính xác suất để:

a) Hộ đó nuôi 2 vật nuôi biết rằng hộ đó có 4 người;

b) Hộ đó có 3 người biết rằng hộ đó có ít nhất 2 vật nuôi;

c) Hộ đó có ít nhất một vật nuôi, biết rằng hộ đó có ít nhất 4 người.

Lời giải chi tiết

a) Gọi A là biến cố: “Hộ đó nuôi 2 vật nuôi”;

B là biến cố: “Hộ đó có 4 người”;

Cần tính \(P\left( {A|B} \right)\).

Ta có \({\rm{ }}n\left( B \right) = 7 + 12 + 11 + 7 = 37,{\rm{ }}n\left( {AB} \right) = 11\).

Do đó \(P\left( B \right) = \frac{{37}}{{98}};{\rm{ }}P\left( {AB} \right) = \frac{{11}}{{98}}\).

Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{11}}{{37}}\).

b) Gọi C là biến cố: “Hộ đó có 3 người”; D là biến cố: “Hộ đó có ít nhất 2 vật nuôi”.

Cần tính \(P\left( {C|D} \right)\).

Ta có \(n\left( D \right) = 29 + 16 = 45;n\left( {CD} \right) = 9 + 3 = 12\).

Do đó \(P\left( D \right) = \frac{{29}}{{98}};P\left( {CD} \right) = \frac{{12}}{{98}}\).

Vậy \(P\left( {C|D} \right) = \frac{{P\left( {CD} \right)}}{{P\left( D \right)}} = \frac{{12}}{{45}} = \frac{4}{{15}}\).

c) Gọi E là biến cố: “Hộ đó có ít nhất một vật nuôi”; F là biến cố: “Hộ đó có ít nhất 4 người”.

Cần tính \(P\left( {E|F} \right)\).

Ta có \(n\left( F \right) = 37 + 12 = 58;n\left( {EF} \right) = 30 + 18 = 48\).

Do đó \(P\left( F \right) = \frac{{58}}{{98}};P\left( {EF} \right) = \frac{{48}}{{98}}\).

Vậy \(P\left( {E|F} \right) = \frac{{P\left( {EF} \right)}}{{P\left( F \right)}} = \frac{{48}}{{58}} = \frac{{24}}{{29}}\).