Giải bài 6.22 trang 27 SGK Toán 10 – Kết nối tri thức
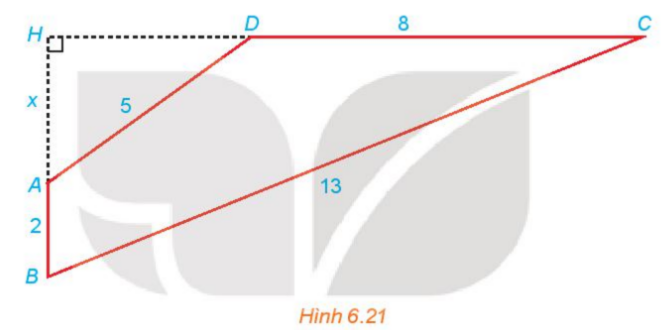
(H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD
Đề bài
Cho từ giác ABCD có \(AB \bot CD;AB = 2;BC = 13;CD = 8;DA = 5\) (H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD
Phương pháp giải - Xem chi tiết
Bước 1: Tính HD,HC theo x
Bước 2: Sử dụng định lý py-ta-go cho tam giác vuông BHC
\(B{C^2} = H{B^2} + H{C^2}\)
Khi đó ta lập được phương trình \(4\sqrt {25 - {x^2}} = - x + 19\)
Bước 3: Giải phương trình trên ta tìm được x
Lời giải chi tiết
Ta có :AH=x (x>0)
Xét tam giác AHD vuông ở H, ta có:
\(A{D^2} = A{H^2} + H{D^2} \Leftrightarrow H{D^2} = A{D^2} - A{H^2} = 25 - {x^2}\)
\( \Rightarrow HD = \sqrt {25 - {x^2}} \)
Ta có: \(HC = HD + DC = \sqrt {25 - {x^2}} + 8\)
\(HB = AH + AB = x + 2\)
Xét tam giác HBC vuông tại H, ta có:
\(\begin{array}{l}B{C^2} = H{B^2} + H{C^2}\\ \Leftrightarrow {13^2} = {(x + 2)^2} + {\left( {\sqrt {25 - {x^2}} + 8} \right)^2}\\ \Leftrightarrow 169 = {x^2} + 4x + 4 + 25 - {x^2} + 16\sqrt {25 - {x^2}} + 64\\ \Leftrightarrow 16\sqrt {25 - {x^2}} = - 4x + 76\\ \Leftrightarrow 4\sqrt {25 - {x^2}} = - x + 19\end{array}\)
Bình phương hai vế của phương trình trên ta được:
\(\begin{array}{l}16(25 - {x^2}) = {x^2} - 38x + 361\\ \Leftrightarrow 17{x^2} - 38x - 39 = 0\end{array}\)
\( \Leftrightarrow x = 3\) hoặc \(x = \frac{{ - 13}}{{17}}\)
Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn
Do x>0 nên ta chọn x=3 => AH=3
\(\begin{array}{l}HD = \sqrt {25 - {3^2}} = 4\\HC = 4 + 8 = 12\\HB = 3 + 2 = 5\end{array}\)
Diện tích tam giác HAD là \({S_1} = \frac{1}{2}.HA.HD = \frac{1}{2}.3.4 = 6\)
Diện tích tam giác HBC là \({S_2} = \frac{1}{2}.HB.HC = \frac{1}{2}.5.12 = 30\)
Vậy diện tích tứ giác ABCD là \(S = {S_2} - {S_1} = 30 - 6 = 24\)