Giải bài 6.8 trang 45 SGK Toán 8 - Cùng khám phá
Cho hình thang (ABCDleft( {AB//CD} right)) có (M) là trung điểm cạnh (AD.)
Đề bài
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(M\) là trung điểm cạnh \(AD.\) Đường thẳng qua \(M\) song song với \(AB\) cắt \(AC\) tại \(P\) và cắt \(BC\) tại \(N.\) Chứng minh rằng:
a) \(P\) là trung điểm của \(AC\) và \(N\) là trung điểm của \(BC;\)
b) \(MN = \frac{1}{2}\left( {AB + CD} \right).\)
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hình thang để chứng minh.
Lời giải chi tiết
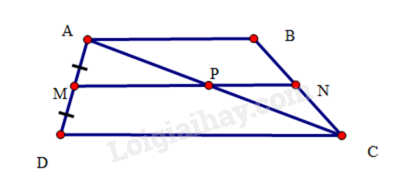
a) Ta có:
\(AB//CD\)
Mà
\(\begin{array}{l}MN//AB\\ = > MN//CD\end{array}\)
Áp dụng hệ quả của tính chất đường trung bình của tam giác: Nếu một đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh còn lại:
Xét tam giác \(ACD\) , ta có:
\(MP//CD\)
M là trung điểm AD
=> P là trung điểm cạnh AC.
Chứng minh tương tự ta có:
P là trung điểm cạnh AC
\(NP//AB\)
=> N là trung điểm cạnh BC.