Giải bài 6 trang 76 sách bài tập toán 10 - Chân trời sáng tạo
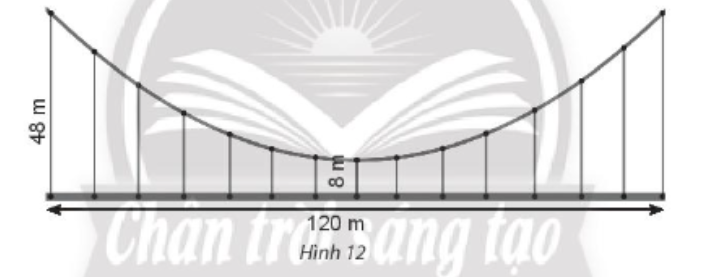
Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 48 m, thanh ngắn nhất là 8 m (Hình 12).
Đề bài
Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 48 m, thanh ngắn nhất là 8 m (Hình 12). Tính chiều dài của thanh cách điểm giữa cầu 20 m.
Phương pháp giải - Xem chi tiết
Parabol \(\left( P \right)\) có dạng \({y^2} = 2px\) với \(p > 0\) có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\), phương trình đường chuẩn \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết
+ Ta chọn hệ tọa độ sao cho parabol có phương trình \({y^2} = 2px\)
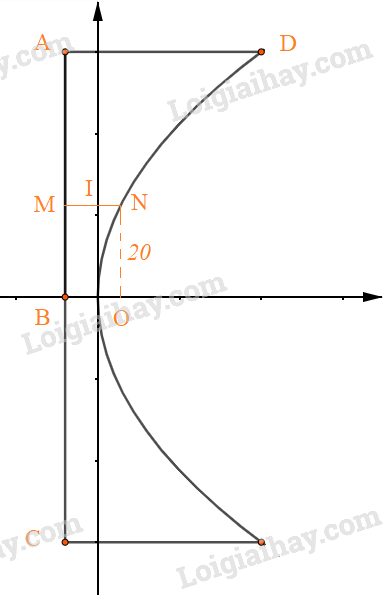
Theo đề bài ta có: \(OB = 8\left( m \right),{\rm{ }}AC = 120\left( m \right),{\rm{ }}AD = 48\left( m \right).\)
\( \Rightarrow B( - 8;0),AB = 60(m)\)
Ta có: \({x_D} = AD - OB = 48 - 8 = 40;{y_D} = AB = 60\)
+ Mà \(D\left( {40;60} \right)\) thuộc parabol
\( \Rightarrow {60^2} = 2.p.40 \Rightarrow p = \frac{{{{60}^2}}}{{80}} = 45\)
Vậy PT parabol đó là \({y^2} = 2.45.x\) hay \({y^2} = 90x\)
+ Điểm giữa cầu là O(0;0), điểm N cách điểm giữa cầu 20 m \( \Rightarrow N\left( {{x_N};20} \right)\), độ dài thanh ngang tương ứng là NM.
\(N\left( {{x_N};20} \right)\) thuộc parabol nên \({20^2} = 90{x_N} \Rightarrow IN = {x_N} = \frac{{{{20}^2}}}{{90}} \approx 4,44m\)
\( \Rightarrow MN = MI + IN = 8 + 4,44 \approx 12,44(m)\)
Vậy chiều dài của thanh cách điểm giữa cầu 20 m là khoảng 12,44 m