Giải bài 62 trang 31 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Mực nước cao nhất tại một cảng biển là 16 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều xuống thấp thì mực nước thấp nhất là 10 m. Đồ thị ở hình bên mô tả sự thay đổi chiều cao của mực nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước \(h\) (m) theo thời gian \(t\)(h) \(\left( {0 \le t \le 24} \right)\) được cho bởi công thức \(h = m + a\cos \left( {\frac{\pi }{{12}}t} \right)\) với \(m\), \(a\) là các số thực dương cho trước.

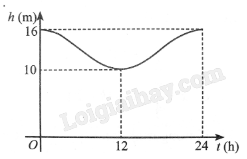
a)    Tìm \(m\), \(a\).

b)    Tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m.

Lời giải chi tiết

a) Do \( - 1 \le \cos \left( {\frac{\pi }{{12}}t} \right) \le 1 \Rightarrow m - a \le h \le m + a\).

Mực nước thấp nhất đạt được là \(m - a\) (m), mực nước cao nhất đạt được là \(m + a\) (m).

Theo đề bài, ta có hệ phương trình: \(\left\{ \begin{array}{l}m - a = 10\\m + a = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 13\\a = 3\end{array} \right.\)

\( \Rightarrow h = 13 + 3\cos \left( {\frac{\pi }{{12}}t} \right)\)

b) Để tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m, ta sẽ giải phương trình: \(h = 11,5 \Leftrightarrow 13 + 3\cos \left( {\frac{\pi }{{12}}t} \right) = 11,5 \Leftrightarrow \cos \left( {\frac{\pi }{{12}}t} \right) = \frac{{ - 1}}{2}\)

\( \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{12}}t = \frac{{2\pi }}{3} + k2\pi \\\frac{\pi }{{12}}t =  - \frac{{2\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 8 + 24k\\t =  - 8 + 24k\end{array} \right.\)\(\left( {k \in \mathbb{Z}} \right)\)

Như vậy, tại thời điểm \(t = 8\)(h) và \(t = 16\)(h), chiều cao của mực nước là 11,5 m.