Giải bài 61 trang 31 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Dùng đồ thị hàm số $y = \sin x$, $y = \cos x$ để xác định số nghiệm của phương trình:

a)    $5\sin x - 3 = 0$ trên đoạn $\left[ { - \pi ;4\pi } \right]$

b)    $\sqrt 2 \cos x + 1 = 0$ trên khoảng $\left( { - 4\pi ;0} \right)$

Lời giải chi tiết

a) Ta có $5\sin x - 3 = 0 \Leftrightarrow \sin x = \frac{3}{5}$.

Nghiệm của phương trình trên chính là hoành độ các giao điểm của đường thẳng $y = \frac{3}{5}$ và đồ thị hàm số $y = \sin x$ như hình vẽ dưới đây.

Dựa vào hình vẽ, ta thấy đường thẳng $y = \frac{3}{5}$ cắt đồ thị hàm số $y = \sin x$ tại 4 điểm có hoành độ nằm trên đoạn $\left[ { - \pi ;4\pi } \right]$. Có nghĩa là, phương trình $5\sin x - 3 = 0$ có 4 nghiệm trên đoạn $\left[ { - \pi ;4\pi } \right]$.

b) Ta có $\sqrt 2 \cos x + 1 = 0 \Leftrightarrow \cos x = \frac{{ - 1}}{{\sqrt 2 }}$

Nghiệm của phương trình trên chính là hoành độ các giao điểm của đường thẳng $y = \frac{{ - 1}}{{\sqrt 2 }}$ và đồ thị hàm số $y = \cos x$ như hình vẽ dưới đây.

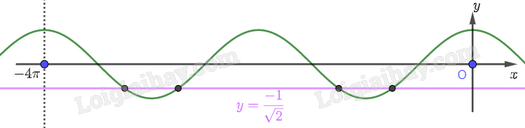
Dựa vào hình vẽ, ta thấy đường thẳng $y = \frac{{ - 1}}{{\sqrt 2 }}$ cắt đồ thị hàm số $y = \cos x$ tại 4 điểm có hoành độ nằm trên khoảng $\left( { - 4\pi ;0} \right)$. Có nghĩa là, phương trình $\sqrt 2 \cos x + 1 = 0$ có 4 nghiệm trên khoảng $\left( { - 4\pi ;0} \right)$.