Giải bài 7.3 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(BD\).
Đề bài
Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(BD\). Biết \(MN = a\sqrt 3 ;AB = 2\sqrt 2 a\) và \(CD = 2a\). Chứng minh rằng đường thẳng \(AB\) vuông góc với đường thẳng \(CD\).
Phương pháp giải - Xem chi tiết
Chứng minh góc giữa đường thẳng \(AB\) và \(CD\) bằng \({90^ \circ }\)
+ Bước 1: Tính góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({90^ \circ }\)
+ Bước 2: Kết luận đường thẳng \(AB\) vuông góc với đường thẳng \(CD\).
Chú ý sử dụng định lý đảo Pytago để chứng minh tam giác là tam giác vuông
Lời giải chi tiết
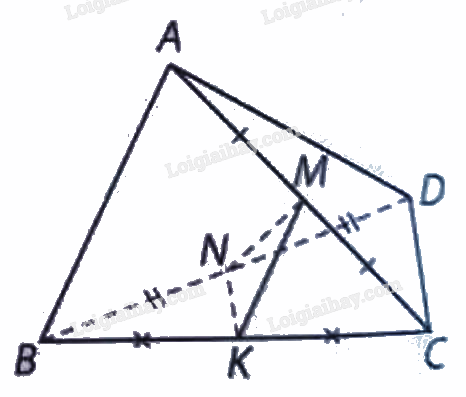
Lấy \(K\) là trung điểm của cạnh \(BC\), ta có: \(NK\) và \(MK\) lần lượt là đường trung bình của tam giác \(BCD\) và tam giác \(ABC\) nên \(NK = a,MK = a\sqrt 2 \).
Do đó, \(M{N^2} = 3{a^2} = N{K^2} + M{K^2}\) suy ra tam giác \(MNK\) vuông tại \(K\), hay \(MK \bot NK\), mà \(MK//AB\) và \(NK//CD\) nên \(\left( {AB,CD} \right) = \left( {MK,NK} \right) = {90^ \circ }\), hay \(AB \bot CD\).