Giải bài 7 trang 61 SGK Toán 10 tập 1 – Cánh diều
Giải các bất phương trình sau:
Đề bài
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
Phương pháp giải - Xem chi tiết
Giải bất phương trình dạng \(f\left( x \right) > 0\).
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của \(f\left( x \right)\)(nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho \(f\left( x \right)\) mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng \(f\left( x \right) < 0,f\left( x \right) \ge 0,f\left( x \right) \le 0\) được giải bằng cách tương tự.
Lời giải chi tiết
a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
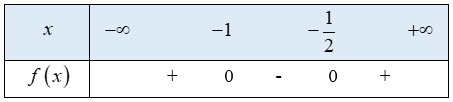
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:
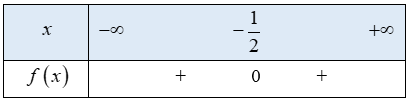
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)