Giải bài 8 trang 35 vở thực hành Toán 9
Trên một khu vườn hình vuông có cạnh bằng 20m người ta làm một lối đi xung quanh vườn có bề rộng x(m) (Hình dưới). Để diện tích lối đi là (76{m^2}) thì bề rộng x là bao nhiêu?
Đề bài
Trên một khu vườn hình vuông có cạnh bằng 20m người ta làm một lối đi xung quanh vườn có bề rộng x(m) (Hình dưới). Để diện tích lối đi là \(76{m^2}\) thì bề rộng x là bao nhiêu?
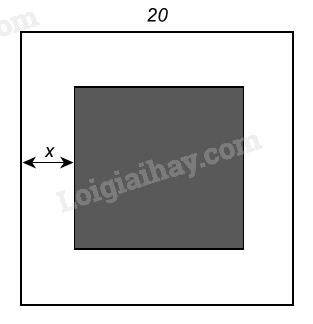
Phương pháp giải - Xem chi tiết
+ Dựa vào dữ kiện đầu bài, lập được phương trình có dạng phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\).
+ Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\), ta giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\). Sau đó lấy tất cả các nghiệm của chúng.
Lời giải chi tiết
Phần đất làm vườn là hình vuông có cạnh \(20 - x\left( m \right)\) và có diện tích đất là \({\left( {20 - x} \right)^2}\;\left( {{m^2}} \right)\)
Theo giả thiết, diện tích đất dành cho làm vườn là: \({20^2} - 76 = 324\left( {{m^2}} \right)\)
suy ra \({\left( {20 - x} \right)^2} = 324\) hay \({\left( {20 - x} \right)^2} = {18^2}\)
\({\left( {20 - x} \right)^2} - {18^2} = 0\)
\(\left( {20 - x - 18} \right)\left( {20 - x + 18} \right) = 0\)
\(\left( {2 - x} \right)\left( {38 - x} \right) = 0\)
Suy ra \(2 - x = 0\) hoặc \(38 - x = 0\)
+) \(2 - x = 0\) hay \( - x = - 2\), suy ra \(x = 2\)
+) \(38 - x = 0\) hay \( - x = - 38\), suy ra \(x = 38\) (loại vì bề rộng của lối đi phải bé hơn cạnh khu vườn)
Vậy bề rộng của lối đi là 2m.