Giải bài 9. 26 trang 81 SGK Toán 7 tập 2 - Kết nối tri thức — Không quảng cáo

Đề bài

Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.

Lời giải chi tiết

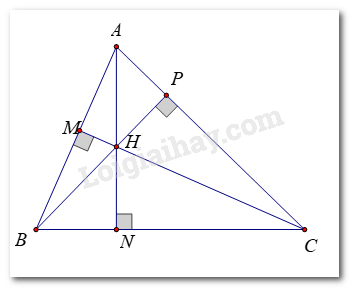
a)

Trong ΔABC ta có H là trực tâm nên:

AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M

Trong ΔAHB, ta có:

HM ⊥ AB

BN ⊥ AH

Mà MH cắt BN tại C

=> C là trực tâm của tam giác AHB.

Trong ΔHAC, ta có:

HP ⊥ AC

CN ⊥ AH

Mà HP cắt CN tại B

=> B là trực tâm của ΔHAC.

Trong ΔHBC, ta có:

HN ⊥ BC

BM ⊥ HC

Mà HN cắt BM tại A

=> A là trực tâm của tam giác HBC.