Giải bài 9.43 trang 60 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho O là trung điểm của đoạn thẳng AB. a) Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A. b) Phép quay thuận chiều ({90^o}) tâm O biến A thành C và biến B thành D. Chứng tỏ rằng ACBD là một hình vuông.
Đề bài
Cho O là trung điểm của đoạn thẳng AB.
a) Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A.
b) Phép quay thuận chiều \({90^o}\) tâm O biến A thành C và biến B thành D. Chứng tỏ rằng ACBD là một hình vuông.
Phương pháp giải - Xem chi tiết
a) Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
b) + Chứng minh tứ giác ABCD nội tiếp đường tròn (O), bán kính \(\frac{{AB}}{2}\).
+ Chứng minh CD là đường kính của (O), suy ra \(\widehat {ACB} = \widehat {CBD} = \widehat {BDA} = \widehat {DAC} = {90^o}\) nên ACBD là hình chữ nhật (1).
+ \(\Delta AOC = \Delta COB = \Delta BOD = \Delta DOA\) nên \(AC = CB = BD = DA\) (2).
+ Từ (1) và (2) suy ra ACBD là hình vuông.
Lời giải chi tiết
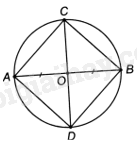
a) Phép quay thuận chiều \({180^o}\) tâm O biến điểm A thành B và biến B thành A.
b) Vì \(OA = OB = OC = OD\) nên tứ giác ABCD nội tiếp đường tròn (O), bán kính \(\frac{{AB}}{2}\).
Vì \(\widehat {AOC} = \widehat {BOD} = {90^o}\) nên OC và OD cùng vuông góc với AB. Do đó, O, C, D thẳng hàng. Suy ra, CD là đường kính của (O). Suy ra, \(\widehat {ACB} = \widehat {CBD} = \widehat {BDA} = \widehat {DAC} = {90^o}\) (các góc nội tiếp chắn nửa đường tròn của (O)). Suy ra, ACBD là hình chữ nhật (1).
Hơn nữa, \(\Delta AOC = \Delta COB = \Delta BOD = \Delta DOA\) (các tam giác vuông cân tại đỉnh O có các cạnh góc vuông bằng nhau) nên \(AC = CB = BD = DA\) (2).
Từ (1) và (2) ta có: ACBD là hình vuông.