Giải bài 9 trang 89 SGK Toán 8 tập 1– Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác $ABC$ cân tại $A$ . Gọi $H$ , $D$ lần lượt là trung điểm của các cạnh $BC$ và $AB$

a) Chứng minh rằng tứ giác $ADHC$ là hình thang

b) Gọi $E$ là điểm đối xứng với $H$ qua $D$ . Chứng minh rằng tứ giác $AHBE$ là hình chữ nhật

c) Tia $CD$ cắt $AH$ tại $M$ và cắt $BE$ tại $N$ . Chứng minh rằng tứ giác $AMBN$ là hình bình hành.

Lời giải chi tiết

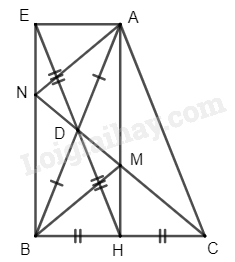
a) Vì $\Delta ABC$ cân tại $A$ nên $\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}$ và $AB = AC$

Vì $\Delta ABC$ cân tại $A$ , có $AH$ là trung tuyến (gt)

Suy ra $AH$ là đường cao

Suy ra $AH \bot BC$

Suy ra $\widehat {{\rm{AHB}}} = \widehat {{\rm{AHC}}} = 90^\circ$

Xét $\Delta AHB$ vuông tại $H$ ta có: $HD$ là trung tuyến

Suy ra $HD = \frac{1}{2}AB$

Mà $DA = DB = \frac{1}{2}AB$ (do $D$ là trung điểm $AB$ )

Suy ra $DA = DB = HD$

Suy ra $\Delta DHB$ cân tại $D$

Suy ra $\widehat {{\rm{ABC}}} = \widehat {{\rm{DHB}}}$

Mà $\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}$ (cmt)

Suy ra $\widehat {{\rm{DHB}}} = \widehat {{\rm{ACB}}}$

Mà hai góc ở vị trí đồng vị

Suy ra $DH$ // $AC$

Suy ra $ADHC$ là hình thang

b) Vì $E$ đối xứng với $H$ qua $D$ (gt)

Suy ra $D$ là trung điểm của $HE$

Xét tứ giác $AHBE$ ta có:

Hai đường chéo $HE$ và $AB$ cắt nhau tại trung điểm $D$

Suy ra $AHBE$ là hình bình hành

Mà $\widehat {{\rm{AHB}}} = 90^\circ$ (cmt)

Suy ra $AHBE$ là hình chữ nhật

c) Vì $AHBE$ là hình chữ nhật (cmt)

Suy ra $AH$ // $BE$ và $AH = BE$

Xét $\Delta DEN$ và $\Delta DHM$ ta có:

$\widehat {{\rm{NED}}} = \widehat {{\rm{DHM}}}$ (do $BE$ // $AH$ )

$DE = DH$ (do $D$ là trung điểm của $HE$ )

$\widehat {{\rm{EDN}}} = \widehat {{\rm{MDH}}}$ (đối đỉnh)

Suy ra $\Delta DEN = \Delta DHM$ (g-c-g)

Suy ra $EN = MH$ (hai cạnh tương ứng)

Mà $BE = AH$ (cmt)

Suy ra $BE - EN = AH - MH$

Suy ra $NB = AM$

Mà $NB$ // $AM$ (do $EB$ // $AH$ )

Suy ra $AMBN$ là hình bình hành