Giải bài tập 10 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo — Không quảng cáo

Đề bài

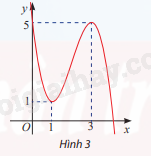
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số

Lời giải chi tiết

Hàm số có dạng: \(y = a{x^3} + b{x^2} + cx + d(a < 0)\)

Đồ thị hàm số giao với Oy tại điểm (0; 5) nên: \(y(0) = a{.0^3} + b{.0^2} + c.0 + d = 5 \Leftrightarrow d = 5\)

Đồ thị hàm số đi qua điểm (3; 5) nên: \(y = a{.3^3} + b{.3^2} + c.3 + 5 = 5 \Leftrightarrow 27a + 9b + 3c = 0\)

Đồ thị hàm số đi qua điểm (1; 1) nên: \(y(1) = a{.1^3} + b{.1^2} + c.1 + 5 = 1 \Leftrightarrow a + b + c =  - 4\)

Ta có: \(y' = 3a{x^2} + 2bx + c\)

Hàm số đạt cực đại tại điểm (3; 5) nên: \(y'(3) = 3a{x^2} + 2bx + c = 3.a{.3^2} + 2.b.3 + c = 0\)\( \Leftrightarrow 27a + 6b + c = 0\)

Ta có hệ phương trình: \(\left\{ \begin{array}{l}27a + 9b + 3c = 0\\a + b + c =  - 4\\27a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b = 6\\c =  - 9\end{array} \right.\)

Vậy hàm số là \(y =  - {x^3} + 6{x^2} - 9x + 5\)