Giải bài tập 9 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo
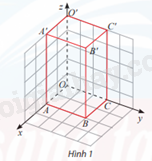
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O′A′B′C′ như Hình 1, biết B′(2; 3; 5). a) Tìm toạ độ các đỉnh còn lại của hình hộp. b) Tính độ dài đường chéo OB′ của hình hộp chữ nhật đó.
Đề bài
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O′A′B′C′ như Hình 1, biết B′(2; 3; 5).
a) Tìm toạ độ các đỉnh còn lại của hình hộp.
b) Tính độ dài đường chéo OB′ của hình hộp chữ nhật đó.
Phương pháp giải - Xem chi tiết
a) Quan sát hình vẽ, mỗi cạnh của ô vuông sẽ tương ứng với 1 đơn vị
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết
a) O(0;0;0), A(2;0;0), B(2;3;0), C(0;3;0), O’(0;0;5), A’(2;0;5), C’(0;3;5)
b) \(\overrightarrow {OB'} = (2;3;5) \Rightarrow OB = \sqrt {{2^2} + {3^2} + {5^2}} = \sqrt {38} \)
Cùng chủ đề:
Giải bài tập 9 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo