Giải bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo
Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B. a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên. b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn? c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?
Đề bài
Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B.
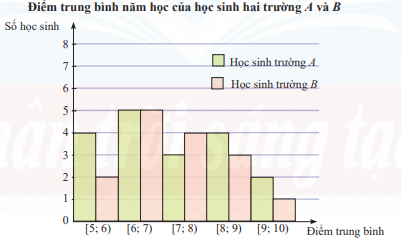a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên.
b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?
c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?
Phương pháp giải - Xem chi tiết
Khi biểu diễn mẫu số liệu liên tục bởi biểu đồ tần số có dạng cột, các cột thường được vẽ kề nhau. Ta quy ước: cột có đầu mút trái là a và có đầu mút phải là b trên trục hoành biểu diễn cho tần số của nhóm [a; b). Giá trị đại diện của nhóm [a; b) là \(c = \frac{1}{2}(a + b)\)
Khoảng tứ phân vị nhỏ hơn thì số giờ nắng trong tháng 6 của địa phương đó đồng đều hơn
Độ lệch chuẩn nhỏ hơn thì số giờ nắng trong tháng 6 của địa phương đó đồng đều hơn
Lời giải chi tiết
a)
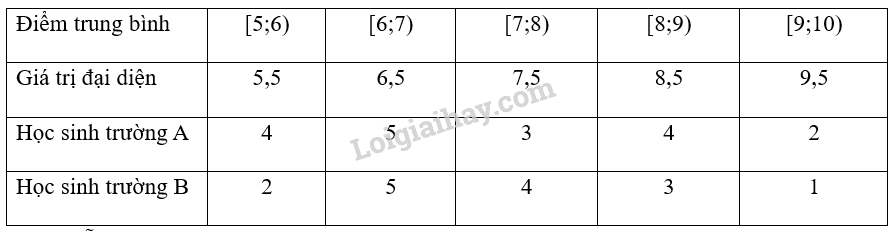
b) Cỡ mẫu: \({n_A} = 18\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{18}}\) là mẫu số liệu gốc về điểm trung bình năm học của học sinh hai trường A được xếp theo thứ tự không giảm.
Ta có: \({x_1};...;{x_4} \in [5;6)\); \({x_5};...;{x_9} \in [6;7)\);\({x_{10}};...;{x_{12}} \in [7;8)\);\({x_{12}}; \ldots ;{\rm{ }}{x_{16}} \in [8;9)\);\({x_{17}};{\rm{ }}{x_{18}} \in [9;10)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_5} \in [6;7)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 6 + \frac{{\frac{{18}}{4} - 4}}{5}(7 - 6) = 6,1\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{14}} \in [8;9)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 8 + \frac{{\frac{{3.18}}{4} - (4 + 5 + 3)}}{4}(9 - 8) = 8,375\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 2,275\)
Cỡ mẫu: \({n_B} = 15\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{15}}\) là mẫu số liệu gốc về điểm trung bình năm học của học sinh hai trường B được xếp theo thứ tự không giảm.
Ta có: \({y_1};{y_2} \in [5;6)\); \({y_3};...;{y_7} \in [6;7)\);\({y_8};...;{y_{11}} \in [7;8)\);\({y_{12}};...;{y_{14}} \in [8;9)\); \({y_{15}} \in [9;10)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_4} \in [6;7)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 6 + \frac{{\frac{{15}}{4} - 2}}{5}(7 - 6) = 6,35\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{12}} \in [8;9)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 8 + \frac{{\frac{{3.15}}{4} - (2 + 5 + 4)}}{3}(9 - 8) = 8,08\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = 1,73\)
Vậy nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn
c) Xét số liệu của trường A:
Số trung bình: \(\overline {{x_X}} = \frac{{4.5,5 + 5.6,5 + 3.7,5 + 4.8,5 + 2.9,5}}{{18}} = 7,22\)
Độ lệch chuẩn: \({\sigma _X} = \sqrt {\frac{{4.5,{5^2} + 5.6,{5^2} + 3.7,{5^2} + 4.8,{5^2} + 2.9,{5^2}}}{{18}} - 7,{{22}^2}} \approx 1,79\)
Xét số liệu của trường B:
Số trung bình: \(\overline {{x_Y}} = \frac{{2.5,5 + 5.6,5 + 4.7,5 + 3.8,5 + 1.9,5}}{{15}} = 7,23\)
Độ lệch chuẩn: \({\sigma _Y} = \sqrt {\frac{{2.5,{5^2} + 5.6,{5^2} + 4.7,{5^2} + 3.8,{5^2} + 1.9,{5^2}}}{{15}} - 7,{{23}^2}} \approx 1,31\)
Vậy nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn