Giải bài tập 17 trang 67 SGK Toán 12 tập 2 - Chân trời sáng tạo
Cho hình hộp chữ nhật (OABC.O'A'B'C'), với (O) là gốc toạ độ, (Aleft( {2;0;0} right)), (Cleft( {0;6;0} right)), (O'left( {0;0;4} right)). Viết phương trình: a) Mặt phẳng (left( {O'AC} right)) b) Đường thẳng (CO') c) Mặt cầu đi qua các đỉnh của hình hộp.
Đề bài
Cho hình hộp chữ nhật \(OABC.O'A'B'C'\), với \(O\) là gốc toạ độ, \(A\left( {2;0;0} \right)\), \(C\left( {0;6;0} \right)\), \(O'\left( {0;0;4} \right)\). Viết phương trình:
a) Mặt phẳng \(\left( {O'AC} \right)\)
b) Đường thẳng \(CO'\)
c) Mặt cầu đi qua các đỉnh của hình hộp.
Phương pháp giải - Xem chi tiết
a) Ta nhận thấy rằng các điểm \(A\), \(C\), \(O'\) lần lượt thuộc các trục toạ độ \(Ox\), \(Oy\), \(Oz\) nên có thể viết phương trình mặt phẳng \(\left( {O'AC} \right)\) dưới dạng phương trình mặt phẳng theo đoạn chắn.
b) Ta có vectơ \(\overrightarrow {CO'} \) là vectơ chỉ phương của đường thẳng \(CO'\), từ đó viết phương trình đường thẳng \(CO'\).
c) Xác định tâm và bán kính của mặt cầu đi qua các đỉnh của hình hộp, từ đó viết phương trình mặt cầu.
Lời giải chi tiết
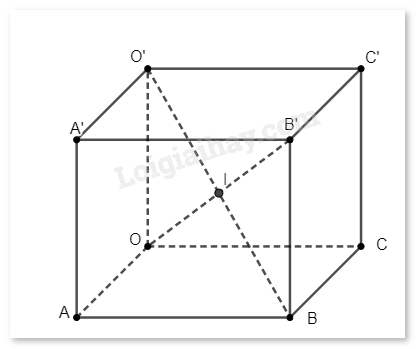
a) Ta thấy rằng các điểm \(A\left( {2;0;0} \right)\), \(C\left( {0;6;0} \right)\), \(O'\left( {0;0;4} \right)\) lần lượt thuộc các trục toạ độ \(Ox\), \(Oy\), \(Oz\), nên phương trình mặt phẳng \(\left( {O'AC} \right)\) là \(\frac{x}{2} + \frac{y}{6} + \frac{z}{4} = 1\), hay \(6x + 2y + 3z - 12 = 0\).
b) Ta có vectơ \(\overrightarrow {CO'} = \left( {0; - 6;4} \right)\) là vectơ chỉ phương của đường thẳng \(CO'\), nên phương trình đường thẳng \(CO'\) là \(\left\{ \begin{array}{l}x = 0 + 0t\\y = 6 - 6t\\z = 0 + 4t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 0\\y = 6 - 6t\\z = 4t\end{array} \right.\)
c) Gọi \(I\) là giao điểm của \(OB'\) và \(O'B\). Ta thấy rằng \(I\) là trung điểm của \(OB'\) và \(O'B\).
Tứ giác \(O'A'BC\) là hình chữ nhật (tứ giác đó là hình bình hành, và hai đường chéo của tứ giác đó cũng là hai đường chéo của hình hộp chữ nhật), nên suy ra \(I\) cũng là trung điểm của \(A'C\). Chứng minh tương tự, ta có \(I\) là trung điểm của \(AC'\).
Vậy ta có điểm \(I\) cách đều 8 đỉnh của hình hộp chữ nhật, nên \(I\) chính là tâm mặt cầu \(\left( S \right)\) đi qua 8 đỉnh đó.
Ta có\(A\left( {2;0;0} \right)\), \(C\left( {0;6;0} \right)\) nên \(B\left( {2;6;0} \right)\).
Ta có \(I\) là trung điểm của \(O'B\) nên \(I\left( {1;3;2} \right)\).
Bán kính của mặt cầu \(\left( S \right)\) là \(R = OI = \sqrt {{1^2} + {3^2} + {2^2}} = \sqrt {14} \)
Vậy phương trình mặt cầu đi qua 8 đỉnh của hình hộp là
\({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 14\).