Giải bài tập 2.7 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính: a) \(\overrightarrow {BC} .\overrightarrow {AH} ;\) b) \(\overrightarrow {AF} .\overrightarrow {EG} ;\) c) \(\overrightarrow {AC} .\overrightarrow {FE} .\)
Đề bài
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính:
a) \(\overrightarrow {BC} .\overrightarrow {AH} ;\)
b) \(\overrightarrow {AF} .\overrightarrow {EG} ;\)
c) \(\overrightarrow {AC} .\overrightarrow {FE} .\)
Phương pháp giải - Xem chi tiết
Để tính tích vô hướng giữa hai vectơ, ta có thể áp dụng công thức:
\(\vec u \cdot \vec v = |\vec u| \cdot |\vec v| \cdot \cos \theta \)
Lời giải chi tiết
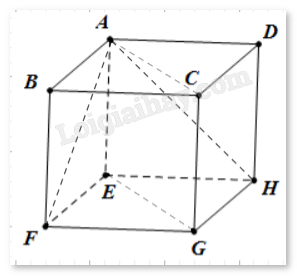
Giả sử hình lập phương ABCD.EFGH có cạnh \(a\).
a) Tính \(\overrightarrow {BC} \cdot \overrightarrow {AH} \):
- \(|\overrightarrow {BC} | = a\)
- \(|\overrightarrow {AH} | = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
- Góc giữa \(\overrightarrow {BC} \) và \(\overrightarrow {AH} \) là \({45^^\circ }\) vì \(\overrightarrow {BC} = \overrightarrow {AD} \) mà \(\widehat {\left( {\overrightarrow {AD} ,\overrightarrow {AH} } \right)} = 45^\circ \)
Do đó:
\(\overrightarrow {BC} \cdot \overrightarrow {AH} = |\overrightarrow {BC} | \cdot |\overrightarrow {AH} | \cdot \cos {45^\circ } = a \cdot a\sqrt 2 \cdot \frac{1}{{\sqrt 2 }} = {a^2}\)
b) Tính \(\overrightarrow {AF} \cdot \overrightarrow {EG} \):
- \(|\overrightarrow {AF} | = a\sqrt 2 \)
- \(|\overrightarrow {EG} | = a\sqrt 2 \)
- Góc giữa \(\overrightarrow {AF} \) và \(\overrightarrow {EG} \) là \({60^\circ }\) vì \(\overrightarrow {EG} = \overrightarrow {AC} \) mà tam giác ACF đều.
Do đó:
\(\overrightarrow {AF} \cdot \overrightarrow {EG} = |\overrightarrow {AF} | \cdot |\overrightarrow {EG} | \cdot \cos {60^\circ } = a\sqrt 2 \cdot a\sqrt 2 \cdot \frac{1}{2} = {a^2}\)
c) Tính \(\overrightarrow {AC} \cdot \overrightarrow {FE} \):
- \(|\overrightarrow {AC} | = a\sqrt 2 \)
- \(|\overrightarrow {FE} | = a\)
- Góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {FE} \) là \({135^\circ }\) vì góc giữa \(\overrightarrow {AC} \) và vectơ đối của \(\overrightarrow {FE} \) là \(\overrightarrow {EF} \) là \(45^\circ \) mà \(\widehat {\left( {\overrightarrow {AC} ,\overrightarrow {EF} } \right)} + \widehat {\left( {\overrightarrow {AC} ,\overrightarrow {FE} } \right)} = 180^\circ \)
Do đó:
\(\overrightarrow {AC} \cdot \overrightarrow {FE} = |\overrightarrow {AC} | \cdot |\overrightarrow {FE} | \cdot \cos {135^\circ } = a\sqrt 2 \cdot a \cdot \cos {135^\circ }\)
Vì \(\cos {135^\circ } = - \frac{1}{{\sqrt 2 }}\), ta có:
\(\overrightarrow {AC} \cdot \overrightarrow {FE} = a\sqrt 2 \cdot a \cdot \left( { - \frac{1}{{\sqrt 2 }}} \right) = - {a^2}\)