Giải bài tập 2. 12 trang 65 SGK Toán 12 tập 1 - Cùng khám phá — Không quảng cáo

Đề bài

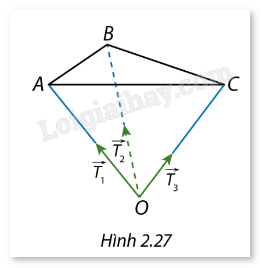
Người ta treo một vật trang trí $O$ có khối lượng $m = 2{\mkern 1mu} {\rm{kg}}$ trên trần nhà bằng các sợi dây nhẹ, không co giãn tại các điểm $A$, $B$ và $C$. Để bảo đảm lực phân phối đều trên các dây và tính thẩm mỹ, người ta chọn độ dài các dây sao cho tứ diện OABC là tứ diện đều. Gọi $\overrightarrow {{T_1}}$, $\overrightarrow {{T_2}}$ và $\overrightarrow {{T_3}}$ lần lượt là các lực căng dây của ba dây treo tại $A$, $B$ và $C$. Lấy giá trị gần đúng của gia tốc trọng trường $g$ là $10{\mkern 1mu} {\rm{m/}}{{\rm{s}}^2}$.

a) Tính cường độ của hợp lực

b) Tính cường độ của lực căng trên mỗi dây.

Lời giải chi tiết

a) Tính cường độ của hợp lực

Trước tiên, ta xác định trọng lực tác dụng lên vật $O$: $\vec P = m \cdot \vec g = 2 \cdot 10 = 20{\mkern 1mu} {\rm{N}}$.

Vì hệ lực đang cân bằng, ta có: $\overrightarrow {{T_1}}  + \overrightarrow {{T_2}}  + \overrightarrow {{T_3}}  + \vec P = \overrightarrow 0$.

Do đó, cường độ của hợp lực bằng trọng lực của vật: $|\vec P| = 20{\mkern 1mu} {\rm{N}}$.

b) Tính cường độ của lực căng trên mỗi dây

Giả sử các lực căng dây có độ lớn bằng nhau $T = |\overrightarrow {{T_1}} | = |\overrightarrow {{T_2}} | = |\overrightarrow {{T_3}} |$, ta có: ${T_{12}} = \sqrt {2{T^2} + 2.{T^2}.\cos 60^\circ }  = T\sqrt 3$ ($\widehat {\left( {\overrightarrow {{T_1}} ,\overrightarrow {{T_2}} } \right)} = 60^\circ$ vì các mặt bên là tam giác đều)

${T_{hl}} = \sqrt {{T_{12}}^2 + {T_3}^2 + 2.{T_{12}}.{T_3}.\cos \alpha }  = \sqrt {3{T^2} + {T^2} + 2.\sqrt 3 T.T.\frac{{\sqrt 3 }}{3}}  = T\sqrt 6$ (phương của $\overrightarrow {{T_{12}}}$ chính là đường trung tuyến của tam giác chứa ${T_1},{T_2}$. Áp dụng định lý Cosin vào tam giác có chứa phương của$\overrightarrow {{T_{12}}}$, phương của $\overrightarrow {{T_3}}$và đường trung tuyến của tam giác đáy để tìm góc giữa $\overrightarrow {{T_{12}}}$$\overrightarrow {{T_3}}$).

Mà: ${T_{hl}} = P = 20$.

Suy ra: $T = \frac{{20}}{{\sqrt 6 }} \approx 8,16$.

Vậy cường độ của lực căng trên mỗi dây là $8,16{\rm{N}}$.