Giải bài tập 2.11 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
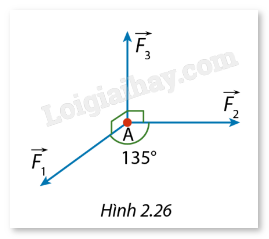
Một chất điểm (A) nằm trên mặt phẳng nằm ngang ((alpha )), chịu tác động bởi ba lực ({vec F_1},{vec F_{{2^prime }}}{vec F_3}). Các lực ({vec F_1},{vec F_2}) có giá nằm trong ((alpha )) và (left( {{{vec F}_1},{{vec F}_2}} right) = {135^circ }), còn lực ({vec F_3}) có giá vuông góc với ( (alpha ) ) và hướng lên trên. Xác định hợp lực của các lực ({vec F_1},{vec F_2},{vec F_3}), biết rằng độ lớn của ba lực đó lần lượt là 20N, 15N và 10N.
Đề bài
Một chất điểm \(A\) nằm trên mặt phẳng nằm ngang \((\alpha )\), chịu tác động bởi ba lực \({\vec F_1},{\vec F_{{2^\prime }}}{\vec F_3}\). Các lực \({\vec F_1},{\vec F_2}\) có giá nằm trong \((\alpha )\) và \(\left( {{{\vec F}_1},{{\vec F}_2}} \right) = {135^\circ }\), còn lực \({\vec F_3}\) có giá vuông góc với ( \(\alpha \) ) và hướng lên trên. Xác định hợp lực của các lực \({\vec F_1},{\vec F_2},{\vec F_3}\), biết rằng độ lớn của ba lực đó lần lượt là 20N, 15N và 10N.
Phương pháp giải - Xem chi tiết
- Các lực \({\vec F_1}\) và \({\vec F_2}\) nằm trong mặt phẳng \((\alpha )\), do đó chúng có thể được cộng trực tiếp để tính hợp lực trong mặt phẳng này.
- Lực \({\vec F_3}\) vuông góc với \((\alpha )\), nên hợp lực tổng sẽ là tổng vectơ của hợp lực \({\vec F_1} + {\vec F_2}\) và \({\vec F_3}\).
- Tính độ lớn của hợp lực \({\vec F_1} + {\vec F_2}\) trong mặt phẳng \((\alpha )\) bằng định lý cosin.
- Tính độ lớn của hợp lực tổng bằng định lý Pythagoras.
Lời giải chi tiết
- Độ lớn của hợp lực \({\vec F_1} + {\vec F_2}\) trong mặt phẳng \((\alpha )\) được tính bằng định lý cosin: \({F_{12}} = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos {{135}^\circ }} \)
Thay số liệu:
\({F_{12}} = \sqrt {{{20}^2} + {{15}^2} + 2 \cdot 20 \cdot 15 \cdot \cos {{135}^\circ }} \)
\({F_{12}} = \sqrt {400 + 225 - 600\frac{{\sqrt 2 }}{2}} = \sqrt {625 - 600\frac{{\sqrt 2 }}{2}} \approx 14,2{\mkern 1mu} {\rm{N}}\)
Tổng hợp lực của \({\vec F_1} + {\vec F_2}\) và \({\vec F_3}\) là: \(F = \sqrt {F_{12}^2 + F_3^2} \)
Thay số liệu: \(F = \sqrt {14,{2^2} + {{10}^2}} \approx 17,3{\mkern 1mu} {\rm{N}}\)