Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám phá
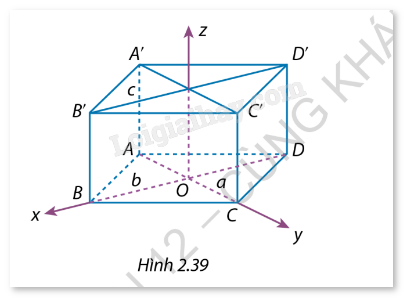
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định: a) Toạ độ các đỉnh của hình hộp; b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).
Đề bài
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định:
a) Toạ độ các đỉnh của hình hộp;
b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).
Phương pháp giải - Xem chi tiết
- Sử dụng gốc tọa độ tại giao điểm của hai đường chéo hình thoi, xác định tọa độ các đỉnh đáy dựa vào chiều dài các đường chéo.
- Dùng công thức \(\overrightarrow {XY} = ({x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1})\) để tìm tọa độ vectơ \(\overrightarrow {BD'} \).
Lời giải chi tiết
a) Xác định tọa độ các đỉnh của hình hộp.
\(B\left( {\frac{b}{2},0,0} \right),{\rm{ }}A\left( {0,\frac{{ - a}}{2},0} \right),C\left( {0,\frac{a}{2},0} \right){\rm{, }}D\left( {\frac{{ - b}}{2},0,0} \right)\)
Tọa độ của các đỉnh A', B', C', D' lần lượt là:
\(B'\left( {\frac{b}{2},0,c} \right),{\rm{ }}A'\left( {0,\frac{{ - a}}{2},c} \right),C'\left( {0,\frac{a}{2},c} \right){\rm{, }}D'\left( {\frac{{ - b}}{2},0,c} \right)\)
b) Tọa độ vectơ \(\overrightarrow {BD'} :\)
\(\overrightarrow {BD'} = D' - B = ( - \frac{b}{2},0,c) - (\frac{b}{2},0,0) = ( - b,0,c)\)