Giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều — Không quảng cáo

Đề bài

Tìm giá trị lớn nhất của mỗi hàm số sau:

a) $f\left( x \right) = \frac{4}{{1 + {x^2}}}$.

b) $f\left( x \right) = x - \frac{3}{x}$ trên nửa khoảng $(0;3]$.

Lời giải chi tiết

a) Tập xác định $D = R$.

Ta có: $f'\left( x \right) = \frac{{8x}}{{{{\left( {1 + {x^2}} \right)}^2}}}$.

Nhận xét $f'\left( x \right) = \frac{{ - 8x}}{{{{\left( {1 + {x^2}} \right)}^2}}} = 0 \Leftrightarrow x = 0$.

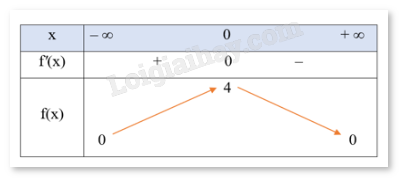
Vậy giá trị lớn nhất của hàm số bằng 4 khi $x = 0$.

b) Ta có: $f'\left( x \right) = 1 + \frac{3}{{{x^2}}}$.

Nhận xét $f'\left( x \right) > 0\forall x \in (0;3]$. Hàm số đồng biến trên (0;3].

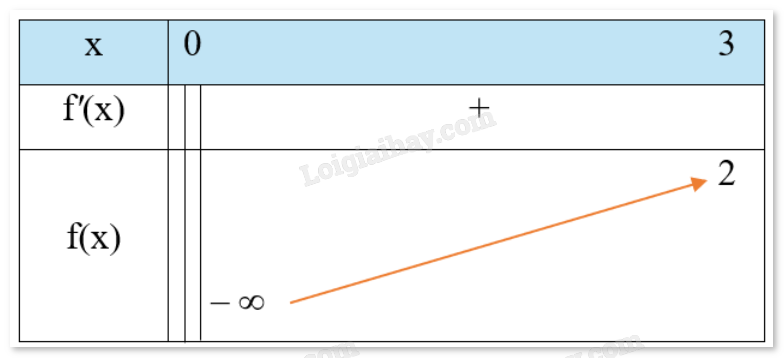
Vậy giá trị lớn nhất của hàm số bằng 2 khi $x = 3$.