Giải bài tập 3. 3 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức — Không quảng cáo

Đề bài

Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.

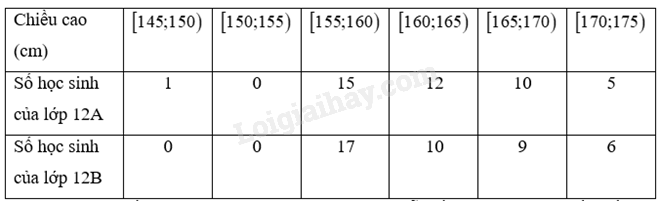a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.

b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?

Lời giải chi tiết

a) Lớp 12A: Khoảng biến thiên: $R = 175 - 145 = 30$

Ta có cỡ mẫu $n = 43$. Giả sử ${x_1},{x_2},...,{x_{43}}$ là chiều cao của các học sinh lớp 12A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.

Vì $\frac{n}{4} = 10,75$ và $1 < 10,75 < 1 + 15$ nên nhóm chứa tứ phân vị thứ nhất là nhóm $\left[ {150;160} \right)$ và tứ phân vị thứ nhất là: ${Q_1} = 155 + \frac{{\frac{{43}}{4} - 1}}{{15}}.5 = 158,25$

Vì $\frac{{3n}}{4} = 32,25$ và $1 + 15 + 12 < 32,25 < 1 + 15 + 12 + 10$ nên nhóm chứa tứ phân vị thứ ba là nhóm $\left[ {165;170} \right)$ và tứ phân vị thứ ba là: ${Q_3} = 165 + \frac{{\frac{{3.43}}{4} - \left( {1 + 15 + 12} \right)}}{{10}}.5 = 167,125$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: ${\Delta _{{Q_1}}} = 167,125 - 158,25 = 8,875$

Lớp 12B: Khoảng biến thiên: $R = 175 - 155 = 20$

Ta có cỡ mẫu $n = 42$. Giả sử ${x_1},{x_2},...,{x_{42}}$ là chiều cao của các học sinh lớp 12B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.

Vì $\frac{n}{4} = 10,5$ và $0 < 10,5 < 17$  nên nhóm chứa tứ phân vị thứ nhất là nhóm $\left[ {155;160} \right)$ và ta có: $Q{'_1} = 155 + \frac{{\frac{{42}}{4} - 0}}{{17}}.5 = \frac{{5375}}{{34}}$

Vì $\frac{{3n}}{4} = 31,5$ và $17 + 10 < 31,5 < 17 + 10 + 9$ nên nhóm chứa tứ phân vị thứ ba là nhóm $\left[ {165;170} \right)$ và tứ phân vị thứ ba là: $Q{'_3} = 165 + \frac{{\frac{{3.42}}{4} - \left( {17 + 10} \right)}}{9}.5 = \frac{{335}}{2}$

Khoảng biến thiên của mẫu số liệu ghép nhóm là: ${\Delta _{{Q_2}}} = \frac{{335}}{2} - \frac{{5375}}{{34}} = \frac{{160}}{{17}}$

b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này, ta nên dùng khoảng tứ phân vị vì khoảng tứ phân vị chỉ phụ thuộc vào nửa giữa của mẫu số liệu, không bị ảnh hưởng bởi các giá trị bất thường.