Giải bài tập 3.2 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau: Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Đề bài
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
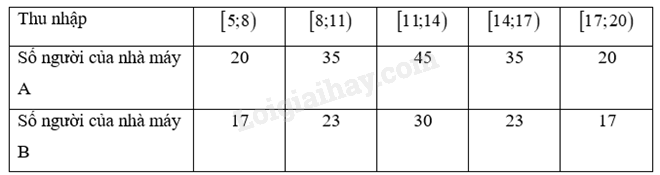
Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng biến thiên của mẫu số liệu ghép nhóm để tính:
Cho mẫu số liệu ghép nhóm:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = {a_{k + 1}} - {a_1}\).
+ Sử dụng kiến thức về khoảng tứ phân vị của mẫu số liệu ghép nhóm để tính: Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết
Ta có bảng số liệu với giá trị đại diện của nhóm là:
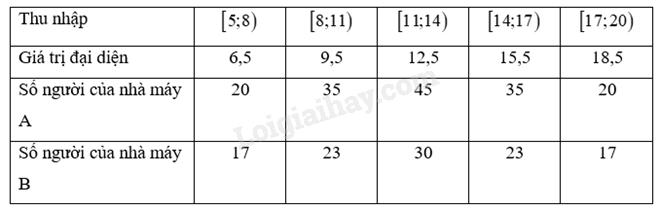
Mức thu nhập trung bình của người lao động nhà máy A là:
\(\frac{{6,5.20 + 9,5.35 + 12,5.45 + 15,5.35 + 18,5.20}}{{20 + 35 + 45 + 35 + 20}} = \frac{{25}}{2}\) (triệu đồng)
Mức thu nhập trung bình của người lao động nhà máy B là:
\(\frac{{6,5.17 + 9,5.23 + 12,5.30 + 15,5.23 + 18,5.17}}{{17 + 23 + 30 + 23 + 17}} = \frac{{25}}{2}\) (triệu đồng)
Nhà máy A: Ta có cỡ mẫu \(n = 155\). Giả sử \({x_1},{x_2},...,{x_{155}}\) là mức thu nhập của người lao động nhà máy A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì \(\frac{n}{4} = 38,75\) và \(20 < 38,75 < 20 + 35\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {8;11} \right)\) và tứ phân vị thứ nhất là: \({Q_1} = 8 + \frac{{\frac{{155}}{4} - 20}}{{35}}.3 = \frac{{269}}{{28}}\)
Vì \(\frac{{3n}}{4} = 116,25\) và \(20 + 35 + 45 < 116,25 < 20 + 35 + 45 + 35\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {14;17} \right)\) và tứ phân vị thứ ba là: \({Q_3} = 14 + \frac{{\frac{{3.155}}{4} - \left( {20 + 35 + 45} \right)}}{{35}}.3 = \frac{{431}}{{28}}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_1}}} = \frac{{431}}{{28}} - \frac{{269}}{{28}} = \frac{{81}}{{14}}\)
Nhà máy B: Ta có cỡ mẫu \(n = 110\). Giả sử \({x_1},{x_2},...,{x_{110}}\) là mức thu nhập của người lao động nhà máy B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì \(\frac{n}{4} = 27,5\) và \(17 < 27,5 < 17 + 23\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {8;11} \right)\) và tứ phân vị thứ nhất là: \(Q{'_1} = 8 + \frac{{\frac{{110}}{4} - 17}}{{23}}.3 = \frac{{431}}{{46}}\)
Vì \(\frac{{3n}}{4} = 82,5\) và \(17 + 23 + 30 < 82,5 < 17 + 23 + 30 + 23\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {14;17} \right)\) và tứ phân vị thứ ba là: \({Q_3} = 14 + \frac{{\frac{{3.110}}{4} - \left( {17 + 23 + 30} \right)}}{{23}}.3 = \frac{{719}}{{46}}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_2}}} = \frac{{719}}{{46}} - \frac{{431}}{{46}} = \frac{{144}}{{23}}\)
Vì \({\Delta _{{Q_1}}} < {\Delta _{{Q_2}}}\) nên mức thu nhập của người lao động nhà máy B biến động nhiều hơn.