Giải bài tập 3 trang 78 SGK Toán 9 tập 2 - Cánh diều
Cho tam giác ABC nội tiếp đường tròn (O) thỏa mãn (widehat {ABC} = 60^circ ,widehat {ACB} = 70^circ .) Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C). Tính số đo góc BDC.
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O) thỏa mãn \(\widehat {ABC} = 60^\circ ,\widehat {ACB} = 70^\circ .\) Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C). Tính số đo góc BDC.
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng Định lý tổng 3 góc trong tam giác ABC để tính góc A.
Bước 2: Áp dụng tổng 2 góc đối trong tứ giác nội tiếp đường tròn bằng \(180^\circ \) để tính góc BDC.
Lời giải chi tiết
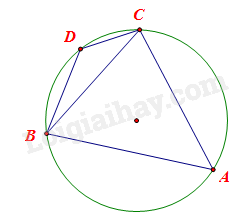
Áp dụng Định lý tổng 3 góc trong tam giác ABC có:
\(\begin{array}{l}\widehat {ABC} + \widehat {BCA} + \widehat {CAB} = 180^\circ \\\widehat {CAB} = 180^\circ - \widehat {ABC} - \widehat {BCA}\\\widehat {CAB} = 180^\circ - 60^\circ - 70^\circ \\\widehat {CAB} = 50^\circ .\end{array}\)
Vì tứ giác ABDC nội tiếp đường tròn nên tổng 2 góc đối bằng \(180^\circ \), do đó ta có:
\(\begin{array}{l}\widehat A + \widehat D = 180^\circ \\\widehat D = 180^\circ - \widehat A\\\widehat D = 180^\circ - 50^\circ \\\widehat D = 130^\circ .\end{array}\)
Vậy \(\widehat {BDC} = 130^\circ .\)