Giải bài tập 6 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khối lượng \(q\) (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán \(p\) (nghìn đồng/kg) theo công thức \(p = 15 - \frac{1}{2}q\). Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức \(R = pq\). a) Viết công thức biểu diễn \(R\) theo \(p\). b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
Đề bài
Khối lượng \(q\) (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán \(p\) (nghìn đồng/kg) theo công thức \(p = 15 - \frac{1}{2}q\). Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức \(R = pq\).
a) Viết công thức biểu diễn \(R\) theo \(p\).
b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
Phương pháp giải - Xem chi tiết
a) Biến đổi công thức \(p = 15 - \frac{1}{2}q\) để tìm biểu thức biểu diễn \(q\) theo \(p\), sau đó thay vào công thức \(R = pq\)
b) Lập hàm số từ công thức trên biểu diễn theo \(p\), tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất
Lời giải chi tiết
a) Ta có: \(p = 15 - \frac{1}{2}q \Leftrightarrow q = 2(15 - p)\)
Thay vào \(R = pq\) ta được: \(R = p.2(15 - p) = - 2{p^2} + 30p\)
b) Đặt \(y = - 2{p^2} + 30p\)
Tập xác định: \(D = (0; + \infty )\)
\(y' = - 4p + 30 = 0 \Leftrightarrow p = 7,5\)
Bảng biến thiên:
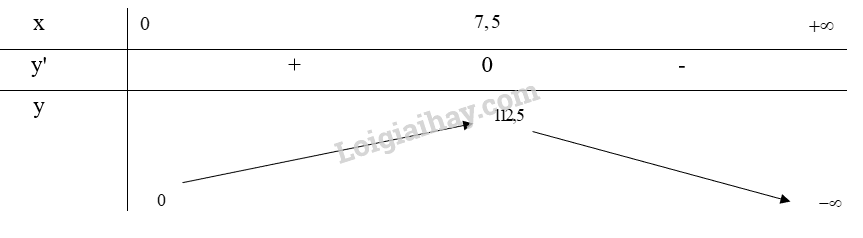
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D y = y(7,5) = 112,5\)
Vậy nếu giá bán mỗi kilôgam sản phẩm là 7,5 nghìn đồng/kg thì sẽ đạt được doanh thu cao nhất là 112,5 nghìn đồng