Giải mục 1 trang 11, 12, 13, 14 SGK Toán 12 tập 2 - Cùng khám phá
Một vật chuyển động thẳng trong 10 giây với vận tốc \(v(t) = 3t + 2\) (m/s). Gọi \(s(t)\) là quãng đường vật đi được đến thời điểm \(t\) giây (0 < t < 10). Xét chuyển động của vật từ thời điểm \(t = 3\) giây đến thời điểm \(t = 5\) giây. a) Giải thích ý nghĩa của đại lượng \(L = s(5) - s(3)\). b) Gọi \(F(t)\) là một nguyên hàm bất kì của \(v(t)\). So sánh \(L\) và \(F(5) - F(3)\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 11 SGK Toán 12 Cùng khám phá
Một vật chuyển động thẳng trong 10 giây với vận tốc \(v(t) = 3t + 2\) (m/s). Gọi \(s(t)\) là quãng đường vật đi được đến thời điểm \(t\) giây (0 < t < 10). Xét chuyển động của vật từ thời điểm \(t = 3\) giây đến thời điểm \(t = 5\) giây.
a) Giải thích ý nghĩa của đại lượng \(L = s(5) - s(3)\).
b) Gọi \(F(t)\) là một nguyên hàm bất kì của \(v(t)\). So sánh \(L\) và \(F(5) - F(3)\).
Phương pháp giải:
a) Đại lượng \(L = s(5) - s(3)\) biểu diễn quãng đường vật đi được từ thời điểm \(t = 3\) giây đến thời điểm \(t = 5\) giây.
b) Ta cần tìm nguyên hàm của hàm vận tốc \(v(t)\) để tìm hàm quãng đường \(s(t)\). So sánh \(L\) với hiệu của giá trị nguyên hàm tại \(t = 5\) và \(t = 3\).
Lời giải chi tiết:
a) \(L = s(5) - s(3)\) là quãng đường mà vật đã đi được từ thời điểm \(t = 3\) giây đến thời điểm \(t = 5\) giây.
b) Ta biết rằng \(s(t)\) là một nguyên hàm của \(v(t) = 3t + 2\). Tính nguyên hàm của \(v(t)\):
\(F(t) = \int {(3t + 2)} {\mkern 1mu} dt = \frac{{3{t^2}}}{2} + 2t + C\)
Do đó:
\(F(5) - F(3) = \left( {\frac{{3{{(5)}^2}}}{2} + 2(5) + C} \right) - \left( {\frac{{3{{(3)}^2}}}{2} + 2(3) + C} \right)\)
\( = \left( {\frac{{75}}{2} + 10} \right) - \left( {\frac{{27}}{2} + 6} \right)\)
\( = \frac{{75 + 20}}{2} - \frac{{27 + 12}}{2} = \frac{{95}}{2} - \frac{{39}}{2} = \frac{{56}}{2} = 28{\rm{ (m)}}\)
Do đó, \(L = F(5) - F(3)\), tức là quãng đường \(s(5) - s(3)\) chính là hiệu của hai giá trị nguyên hàm tại hai thời điểm tương ứng.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 11 SGK Toán 12 Cùng khám phá
Gọi \((H)\) là hình thang vuông giới hạn bởi đường thẳng \(y = 2x + 1\), trục hoành và hai đường thẳng \(x = 1\), \(x = t\) (1 ≤ t ≤ 4) (Hình 4.3a).
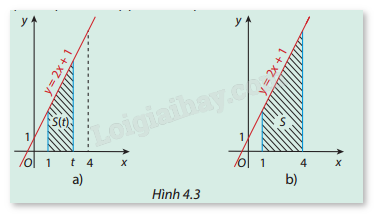
a) Tính diện tích \(S\) của hình \((H)\) khi \(t = 4\) (Hình 4.3b).
b) Tìm hàm số \(S(t)\) biểu thị diện tích của hình \((H)\) với \(t \in [1;4]\).
c) Chứng minh \(S(t)\) là một nguyên hàm của hàm số \(f(t) = 2t + 1\) trên đoạn [1; 4] và \(S = S(4) - S(1)\).
Phương pháp giải:
a) Tính diện tích hình thang vuông bằng công thức trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy, tuy nhiên chiều cao ở đây chính là cạnh bên vuông góc với cả 2 đáy. Trong trường hợp này thì độ dài chiều cao sẽ là khoảng cách từ \({x_1}\) đến \({x_2}\) và độ dài hai cạnh đáy sẽ là giá trị của \(y\) tại hai điểm \({x_1}\) và \({x_2}\).
b) Xét diện tích hình thang tổng quát khi \(t\) thay đổi, tìm hàm số diện tích \(S(t)\).
c) Chứng minh bằng cách lấy đạo hàm của hàm số \(S(t)\) và so sánh với \(f(t)\).
Lời giải chi tiết:
a) Khi \(t = 4\), diện tích của hình thang vuông \((H)\) là:
\(S = \frac{1}{2} \times ({y_1} + {y_2}) \times ({x_2} - {x_1})\)
Trong đó: \({y_1} = 2(1) + 1 = 3\) \({y_2} = 2(4) + 1 = 9\) \({x_1} = 1\), \({x_2} = 4\).
Do đó:
\(S = \frac{1}{2} \times (3 + 9) \times (4 - 1) = \frac{1}{2} \times 12 \times 3 = 18\) (đơn vị diện tích)
b) Diện tích hình thang tổng quát khi \(t\) thay đổi từ 1 đến 4:
\(S(t) = \frac{1}{2} \times ({y_1} + y(t)) \times (t - 1)\)
Trong đó: \({y_1} = 3\) \(y(t) = 2t + 1\) \({x_1} = 1\), \({x_2} = t\) Do đó:
\(S(t) = \frac{1}{2} \times (3 + 2t + 1) \times (t - 1) = \frac{1}{2}S(t) = \frac{1}{2} \times (2t + 4) \times (t - 1)\)
\(S(t) = (t + 2) \times (t - 1) = {t^2} - t + 2t - 2 = {t^2} + t - 2\)
c) Chứng minh \(S(t)\) là nguyên hàm của hàm \(f(t) = 2t + 1\):
\(S(t) = {t^2} + t - 2\)
Lấy đạo hàm của \(S(t)\):
\(S'(t) = 2t + 1 = f(t)\)
Do đó, \(S(t)\) là nguyên hàm của \(f(t) = 2t + 1\). Cuối cùng, diện tích \(S = S(4) - S(1)\) được tính như sau:
\(S(4) = {4^2} + 4 - 2 = 16 + 4 - 2 = 18\)
\(S(1) = {1^2} + 1 - 2 = 1 + 1 - 2 = 0\)
\(S = 18 - 0 = 18\) (đơn vị diện tích).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 13 SGK Toán 12 Cùng khám phá
Cho hàm số \(f(x) = 2x\).
a) Tìm các hàm số \(F(x),G(x)\) là nguyên hàm của \(f(x)\) trên đoạn \([a;b].\)
b) So sánh \(F(b) - F(a)\) và \(G(b) - G(a)\).
Phương pháp giải:
a)
- Nguyên hàm của một hàm số \(f(x)\) là một hàm số \(F(x)\) sao cho \(F'(x) = f(x)\).
- Để tìm nguyên hàm của \(f(x)\), ta thực hiện việc tích phân \(f(x)\) theo \(x\).
b)
- Hai nguyên hàm của cùng một hàm số \(f(x)\) chỉ khác nhau một hằng số, nghĩa là nếu \(F(x)\) và \(G(x)\) đều là nguyên hàm của \(f(x)\), thì \(F(x) = G(x) + C\) với \(C\) là một hằng số. Từ đó, tính hiệu \(F(b) - F(a)\) và \(G(b) - G(a)\) để so sánh.
Lời giải chi tiết:
a) Xét hàm số \(f(x) = 2x\). Nguyên hàm của \(f(x)\) được tính bằng cách tích phân:
\(F(x) = \int 2 x{\mkern 1mu} dx\)
Áp dụng công thức tích phân:
\(F(x) = \int 2 x{\mkern 1mu} dx = {x^2} + {C_1}\)
Trong đó, \({C_1}\) là hằng số tích phân. Tương tự, ta có thể tìm một nguyên hàm khác của \(f(x)\):
\(G(x) = \int 2 x{\mkern 1mu} dx = {x^2} + {C_2}\)
Trong đó, \({C_2}\) là một hằng số khác. Như vậy, hai nguyên hàm của \(f(x)\) có dạng:
\(F(x) = {x^2} + {C_1}\)
\(G(x) = {x^2} + {C_2}\)
b)
Ta có:
\(F(b) - F(a) = \left( {{x^2} + {C_1}} \right)|_{x = a}^{x = b} = ({b^2} + {C_1}) - ({a^2} + {C_1}) = {b^2} - {a^2}\)
Và:
\(G(b) - G(a) = \left( {{x^2} + {C_2}} \right)|_{x = a}^{x = b} = ({b^2} + {C_2}) - ({a^2} + {C_2}) = {b^2} - {a^2}\)
Từ đây, dễ thấy rằng:
\(F(b) - F(a) = G(b) - G(a) = {b^2} - {a^2}\)
Kết luận: Mặc dù \(F(x)\) và \(G(x)\) là hai hàm khác nhau, nhưng hiệu \(F(b) - F(a)\) và \(G(b) - G(a)\) luôn bằng nhau, và đều bằng \({b^2} - {a^2}\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 14 SGK Toán 12 Cùng khám phá
Tính
a) \(\int\limits_1^3 {{x^3}dx;} \)
b) \(\int\limits_0^\pi {\cos udu.} \)
Phương pháp giải:
- Tìm nguyên hàm của hai hàm số.
- Áp dụng công thức của tích phân xác định:
\(\int\limits_a^b f (x){\mkern 1mu} dx = F(b) - F(a)\)
trong đó, \(F(x)\) là nguyên hàm của \(f(x)\).
Lời giải chi tiết:
a)
Tìm nguyên hàm của \({x^3}\):
\(\int {{x^3}} {\mkern 1mu} dx = \frac{{{x^4}}}{4} + C\)
Do đó, nguyên hàm của \(f(x) = {x^3}\) là \(F(x) = \frac{{{x^4}}}{4}\). Áp dụng công thức tính tích phân xác định:
\(\int\limits_1^3 {{x^3}} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4}} \right]_1^3\)
Thay giá trị \(x = 3\) và \(x = 1\) vào nguyên hàm:
\(\int\limits_1^3 {{x^3}} {\mkern 1mu} dx = \frac{{{3^4}}}{4} - \frac{{{1^4}}}{4} = \frac{{81}}{4} - \frac{1}{4} = \frac{{80}}{4} = 20\)
Kết quả:
\(\int\limits_1^3 {{x^3}} {\mkern 1mu} dx = 20\)
b)
Tìm nguyên hàm của \(\cos u\):
\(\int {\cos } u{\mkern 1mu} du = \sin u + C\)
Do đó, nguyên hàm của \(f(u) = \cos u\) là \(F(u) = \sin u\). Áp dụng công thức tính tích phân xác định:
\(\int\limits_0^\pi {\cos } u{\mkern 1mu} du = \left[ {\sin u} \right]_0^\pi \)
Thay giá trị \(u = \pi \) và \(u = 0\) vào nguyên hàm:
\(\int\limits_0^\pi {\cos } u{\mkern 1mu} du = \sin (\pi ) - \sin (0) = 0 - 0 = 0\)
Kết quả:
\(\int\limits_0^\pi {\cos } u{\mkern 1mu} du = 0\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 14 SGK Toán 12 Cùng khám phá
Cho \(F(x)\) là một nguyên hàm của hàm \(f(x) = {2^x}\) và \(F(0) = 0\). Tính \(F(1)\).
Phương pháp giải:
- Tìm nguyên hàm của hàm số \(f(x) = {2^x}\):
- Áp dụng công thức của tích phân xác định để tìm \(F(1)\)
\(\int\limits_a^b f (x){\mkern 1mu} dx = F(b) - F(a)\)
trong đó, \(F(x)\) là nguyên hàm của \(f(x)\).
Lời giải chi tiết:
Tìm nguyên hàm của \(f(x) = {2^x}\):
\(F(x) = \int {{2^x}} {\mkern 1mu} dx\)
Sử dụng công thức tích phân của hàm số mũ, ta có:
\(F(x) = \frac{{{2^x}}}{{\ln 2}} + C\)
Áp dụng công thức tính tích phân xác định, ta có:
\(\int\limits_0^1 f (x){\mkern 1mu} dx = F(1) - F(0)\)
Suy ra:
\(F(1) = \int\limits_0^1 {f(x)} + F(0) = \frac{{{2^1}}}{{\ln 2}} - \frac{{{2^0}}}{{\ln 2}} + 0 = \frac{1}{{\ln 2}}\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 14 SGK Toán 12 Cùng khám phá
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = \sqrt x \), trục hoành và các đường thẳng \(x = 1\), \(x = 4\). (Hình 4.6).
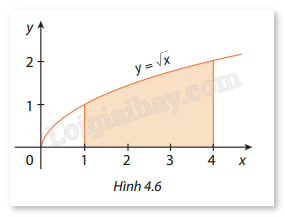
Phương pháp giải:
- Thiết lập tích phân để tính diện tích hình thang cong:
\(S = \int_1^4 {\sqrt x } {\mkern 1mu} dx\)
- Tính tích phân xác định từ 1 đến 4 của hàm \(\sqrt x \).
Lời giải chi tiết:
Thiết lập tích phân:
\(S = \int_1^4 {\sqrt x } {\mkern 1mu} dx = \int_1^4 {{x^{1/2}}} {\mkern 1mu} dx\)
Tính tích phân:
\(\int {{x^{1/2}}} {\mkern 1mu} dx = \frac{{{x^{3/2}}}}{{3/2}} + C = \frac{2}{3}{x^{3/2}} + C\)
Do đó, diện tích cần tìm là:
\(S = \left[ {\frac{2}{3}{x^{3/2}}} \right]_1^4 = \frac{2}{3}\left[ {{4^{3/2}} - {1^{3/2}}} \right]\)
Tính giá trị cụ thể:
\({4^{3/2}} = {({2^2})^{3/2}} = {2^3} = 8\)
\(S = \frac{2}{3}(8 - 1) = \frac{2}{3} \times 7 = \frac{{14}}{3}\)