Giải mục 1 trang 15, 16 SGK Toán 12 tập 1 - Cùng khám phá
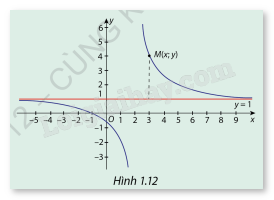
Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong ( Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y=1 khi \(x \to + \infty \) và \(x \to - \infty \).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong ( Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y=1 khi \(x \to + \infty \) và \(x \to - \infty \).
Phương pháp giải:
Nhìn đồ thị hàm số rồi nhận xét.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy:
Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng y=1 càng nhỏ.
LT1
Trả lời câu hỏi Luyện tập 1 trang 16 SGK Toán 12 Cùng khám phá
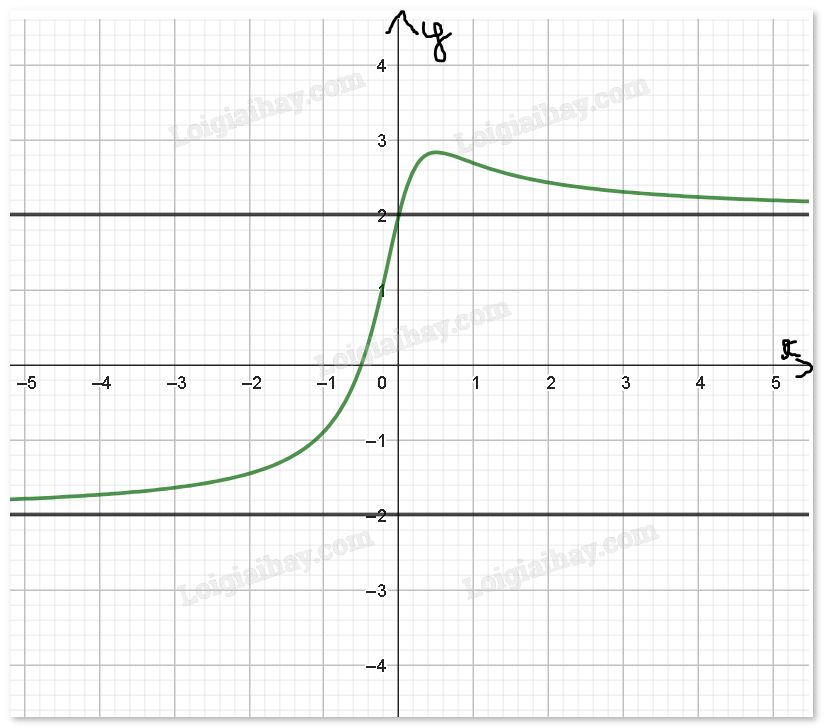
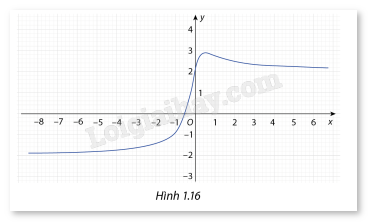
Cho hàm số \(y = f(x) = \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\) có đồ thị như Hình 1.16
a) Tìm các đường tiệm cận ngang của đô thị nếu có.
b) Vẽ các đường tiệm cận ngang vừa tìm được nếu có.
Phương pháp giải:
a) Xét \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to - \infty } f(x)\)
b) Trên trục Oy tại điểm có giá trị bằng 2 vẽ một đường thẳng song song với Ox. Trên trục Oy tại điểm có giá trị bằng -2 vẽ một đường thẳng song song với Ox.
Lời giải chi tiết:
a) Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = 2.
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = - 2.
b)